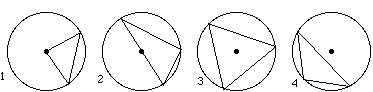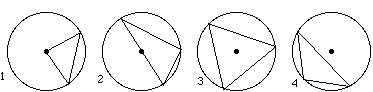www.MathEd.page/angles
Adapted from Geometry Labs, by Henri Picciotto
Angles and Triangles in a Circle
Equipment: Circle Geoboard, Circle Geoboard Paper
|
Types of triangles:
|
| Equilateral (EQ) |
Acute Isosceles (AI) |
| Right Isosceles (RI) |
Obtuse Isosceles (OI) |
| Acute Scalene (AS) |
Right Scalene (RS) |
| Half-Equilateral (HE) |
Obtuse Scalene (OS) |
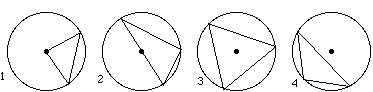
- Make triangles on the circle geoboard, with one vertex at the center and the other two on the circle. (See circle 1 above.)
- Make one of each of the eight types of triangles listed above, if possible. You do not have to do them in order!
- Sketch one of each of the types of triangles it was possible to make on circle geoboard paper. Identify which type of triangle it is, and label all three of its angles with their measures in degrees. (Do not use a protractor! Use geometry to figure out the angles.)
- Thinking back:
- What is true of all the possible triangles in Problem 1?
- Summarize your strategy for finding the angles. Describe any shortcuts or formulas you used.
Definition: A triangle is inscribed in a circle if all three of its vertices are on the circle.
- Repeat Problem 1 with inscribed triangles such that the circle's center is on a side of the triangle. (See circle 2.) Hint: Drawing an additional radius should help you find the measures of the angles.
- Thinking back:
- Summarize your strategy for finding the angles. Describe any shortcuts or formulas.
- Write the exterior angle theorem. How can it be used to help find the angles?
- What is true of all the possible triangles in Problem 3? Prove your answer.
- Repeat Problem 1 with inscribed triangles such that the circle's center is inside the triangle. (See circle 3.)
- Repeat Problem 1 with inscribed triangles such that the circle's center is outside the triangle. (See circle 4.)
Discussion
- Which triangles are impossible in Problem 1? Why?
- In Problem 1, what is the smallest possible angle at the vertex that is at the circle's center? Explain.
- Explain why the angle you found in Question B is the key to Problem 1.
- How do you use the isosceles triangle theorem to find the other two angles of the triangles in Problem 1?
- What is true of all the triangles in Problem 6? All the triangles in Problem 7? Explain.