/circle/hyp-ratios.html
Adapted from Geometry Labs, by Henri Picciotto
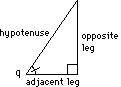
In the previous two activities, we were working with three numbers: the two legs of a right triangle (which we thought of as rise and run) and an angle. Given any two of those, it was possible to find the third. However, in some right triangle situations, the three numbers you need to deal with could be the hypotenuse, one leg, and an angle. To address such problems, we will use two ratios involving the hypotenuse:
![]()
Using your ten-centimeter circle, find these ratios and angles and fill out the tables:
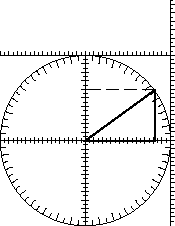
| q | opp/hyp | adj/hyp |
| 0° | ||
| 15° | ||
| 30° | ||
| 45° | ||
| 60° | ||
| 75° | ||
| 90° |
| opp/hyp | q | adj/hyp | q | |
|---|---|---|---|---|
| 0 |
0 | |||
| .2 | .2 | |||
| .4 | .4 | |||
| .6 | .6 | |||
| .8 | .8 | |||
| 1 | 1 |