/circle/slope-angles.html
Adapted from Geometry Labs, by Henri Picciotto
The ten-centimeter circle includes ruler and protractor markings.
Think of the line with equation y = mx, and of the angle q it makes with the positive x-axis. Each slope m corresponds to a certain angle. You can think about this relationship by drawing a right triangle on your 10-cm circle like one of those shown below. The legs give the rise and run for the slope of the hypotenuse. You can read off the angle where the hypotenuse crosses the protractor to find the angle that corresponds to a given slope. Note that even though both the examples below show positive slopes, you can use the circle geoboard to find the angles corresponding to negative slopes as well.
| m | q |
|---|---|
| 0 | |
| .2 | |
| .4 | |
| .6 | |
| .8 | |
| 1 | |
| 1.25 | |
| 1.67 | |
| 90° | |
| -5 | |
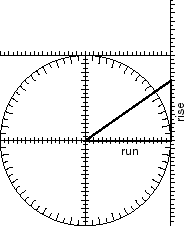
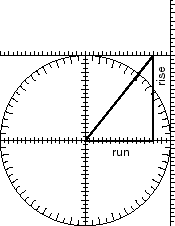
In Problem 4, you found angles that correspond to given slopes. You can also find slopes that correspond to given angles. Two examples of how to do this are shown below. In the example below left, you can read rise off the y-axis and run off the x-axis. In the example below right, a line is drawned at 30°, past the right edge. You can read rise off the right edge ruler. (What would run be in that example?)
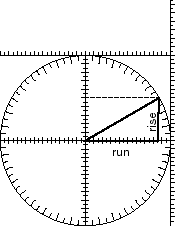
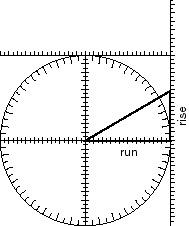
| q | m |
|---|---|
| 0° | |
| 15° | |
| 30° | |
| 45° | |
| 60° | |
| 75° | |
| 90° | |
| 105° | |
| 120° | |
| 135° | |
| 150° | |
| 165° | |
| 180° |