My news:
- I am currently updating the Lab Gear books for Didax. I expect the new version will be available for purchase by this spring. The blocks are available now.
- I offered several workshops last summer. The handouts, links, GeoGebra files, and other info from those will be available for another few weeks here.
- I hope to find some venues for workshops this summer. As it stands now, I have a couple of possibilities, but nothing is confirmed yet. Likely topics are Visual Algebra and Transformational Geometry, consistent with the Common Core.
On to the newsletter!

Blog Posts
Here are links to posts on my Math Education Blog that you might find interesting.
If you are so moved, you may comment on the posts, and/or subscribe to the blog.
Patterns
A correspondent raised an interesting question: we encourage students to look for patterns. Isn't there a risk that they will believe a pattern is a proof? Or that a given pattern is not merely a clue that something is going on, but in fact the cause of it? In fact, yes, that's a risk, and as students grow in age and mathematical sophistication, it behooves us to discuss this explicitly. But this does not take anything away from the fact that pattern-seeking is an important mathematical habit of mind, which should by all means remain in our toolkit. Find a more thorough discussion of this, with examples, here.
What Do You Notice?
However, one use of pattern-seeking that I deem ineffective is found in an extremely widespread misuse of graphing technology. The way it works is that students are asked to graph something, then something else, and so on, and then they are asked "What do you notice?" In this situation, creating patterns is preferable to noticing them. In my Make These Designs activity, I propose an approach that requires students to engage on a deeper level. This may well be my most popular piece of curriculum, both among teachers and students, perhaps because it is a creative and "constructionist" activity, to use the word coined by Seymour Papert. Read about it here.
(Note that there is a similar issue when using interactive geometry software. In that context, the answer lies in asking students to take on increasingly challenging geometric construction challenges. Find a construction unit here.)
Proportional Relationships
Proportional relationships is of course a huge topic in middle school, as it should be. I gave some thought to the real world and mathematical contexts which can be used to illustrate it, to what learning tools are available to teach it, and to how it connects to other concepts. I arranged all this in a themes, tools, concepts map. It was a fun exercise, which could be done about any school topic, and which can be helpful when brainstorming about teaching that topic. It can be the start of "forward design," and yield a far richer curriculum than the reductive strategy of starting with quiz questions and working backwards. The key point is that there is not just one way to teach this, or anything, let alone a best way. A solid curriculum needs to navigate between many ingredients. See the proportional relationships map and some discussion of it here.
MathEducation.page
New on my Web site.
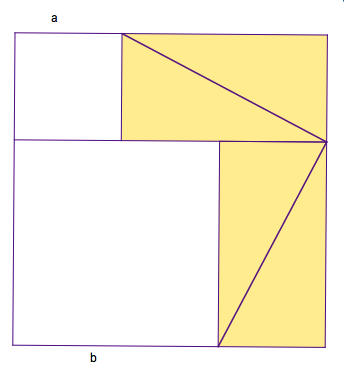
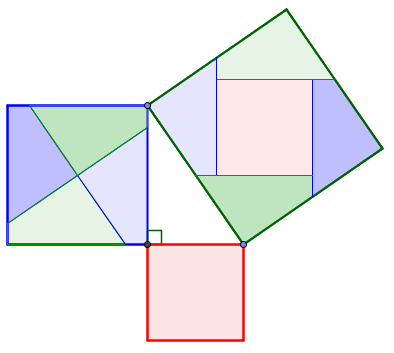
Pythagorean Proofs
I have now animated three proofs of the Pythagorean theorem. (Start here.) I also wrote some notes on how you might use them in the classroom.
Interactive Whiteboards
The most visited post on my blog is my explanation of why and how using the interactive whiteboard is not in conflict with my philosophy of student-centered instruction. I have now added a much improved, expanded, and illustrated article on this topic to my Web site, along with a short video that illustrates a couple of the points I make in the article. Click here.
Transformational Geometry and Triangle Similarity
A recurrent topic in this newsletter is transformational geometry, in part because it is a key concept in the Common Core. One result about dilations is foundational: the image of a line segment in a dilation with factor k is parallel to the original segment, and k times as long. Because the only proof I had seen of this was epic and inappropriate for secondary school, my view was that it should be accepted without proof. This is what I recommended in my paper on how to derive the triangle congruence and similarity criteria on a basis of transformations.
Since then, my friend and colleague Lew Douglas came up with a wonderful proof of it, which is definitely suitable for teachers and curriculum developers. We combined his proof and his approach to similarity with what I had done on congruence into a brand new document. You can find it near the bottom of my Transformational Geometry page. How all this translates into actual curriculum remains to be worked out, but our paper offers a strong framework.