I have recently retired from teaching high school math in an independent school, and now work largely with public schools, as a freelance math education consultant and curriculum developer. If I were still in the classroom, I could have ignored the Common Core State Standards for Mathematics (CCSSM) for a while, because their impact on private schools would take some time to kick in. However in my new career, the CCSSM affect everything I do, so I decided to take a close look at the standards for grades 9-12.

The views I articulate in this paper are based on my own experience as a teacher (42 years in the classroom, K-12), curriculum developer (author of a dozen books, a dozen articles, and a large math education website), and department chair (30 years or so at the Urban School of San Francisco.) I realize that this does not guarantee that I am right about any of the questions I'll be addressing. On the other hand, I am confident that my experience is at least as valid as that of any one of the authors of the CCSSM.

My Background

As a department chair, I led a long-term project of developing a curriculum (and pedagogy) that would work with a wide range of students. While the Urban School is a private school and does not have to contend with the challenges of teaching students from an economically disadvantaged background, our incoming student SSAT scores covered a huge range. At one point a few years ago, one quarter of our entering students scored between the 10th and the 50th percentile, half scored between the 50th and the 80th, and one quarter between the 80th and 99th. All these students attended the same untracked core classes, and then chose among a wide range of electives. All of them went to college, and the top tier went to top universities.

This experience with a somewhat diverse student body was combined with a highly collaborative department, a commitment to student-centered learning that prioritized understanding, an openness to the use of tools (manipulative and technological), and a supportive administration. Moreover, we were not particularly attached to tradition, and this made it possible for us to boldly implement changes that would be more difficult to carry out in a different environment. As a private school, we were under parental and societal pressures to achieve results, so even without endless testing, there is no question we were "accountable."

In this context, I was able to develop curriculum materials that have been useful to teachers in a wide range of schools, and some of it has directly or indirectly inspired curricula with a much wider reach. I hope that this paper is similarly useful to the broader math education community. It is the outcome of a close reading of the Common Core State Standards for high school math, which I compared with a practice I know to be effective.

My Biases

For better or for worse, writing about math education is inherently political, so I might as well state my biases up front:

- Equity: I believe that taught properly, math can be fun, interesting, and useful to all students.

- Technology: I believe that speed and accuracy in paper-pencil computation are no longer valid priorities in math education, and that all students deserve full access to all relevant technological tools.

- Curriculum: I believe that a teacher's knowledge and attitudes about math and pedagogy are more important than the choice of curriculum. (Though I do like the lessons and activities I created!)

- Pedagogy: I believe that the art of teaching lies in being flexible and eclectic.

- Against oversimplification. All claims to having discovered "the way" are spurious. Everything in math education is more complicated than one might think, and there is no one way.

This last point means that I am loath to take a blanket position for or against the Common Core. National standards are neither a good nor a bad thing in principle. It all depends on the standards themselves, on their scope, and on their implementation. In this paper, I will present what I see as the good, the bad, and the ugly aspects of the CCSSM and I will end with some proposals for math educators.

I should make clear right from the start that this is an opinion piece, based solely on my experience and beliefs. Perhaps I should have surveyed what has been written on this subject, but I’ll leave this to the scholars.

II. The Good

The Big Picture

The self-proclaimed goals of the CCSSM are worthy of support. Those include:

Coherence: Instead of the helter-skelter sequencing of traditional school mathematics, the standards are intended to follow a meaningful sequence across the grades (while not mandating a sequence within each grade.)

Focus: Instead of touching on too many topics superficially each year, and having to revisit them year after year, the idea is to teach fewer things in a given year, in more depth. This may make it possible to learn something one year, and move on to something else the following year.

Redefinition of rigor: "Rigor", which was once the club wielded by some against any attempt at teaching for understanding, is being redefined to have three elements: conceptual understanding, procedural fluency, and practical application.

Standards for Mathematical Practice (SMP): Those are intended as integral to the whole. They focus on student disposition and habits of mind, and are meant to inseparable from the content standards.

I welcome the fact that quite a few leaders on both sides of the math wars have managed to reach a bit of a truce around the CCSSM. This is seen by some of their supporters as betrayal, but our time is better spent teaching and developing curriculum than engaging in futile debates. I have been viciously attacked by traditionalists, and have engaged in those skirmishes, but in the end I don't think much was accomplished that way.

Another good thing is that some excellent curriculum materials are being developed and made available to teachers for free in order to support the CCSSM. Moreover, substantial numbers of teachers seem to be getting involved in learning about those and growing professionally as a result.

In addition, having a single set of national guidelines prevents large states from having an undue influence over what is taught all over the country, through their impact on publishers’ bottom line.

Finally, and crucially, it is one way to guard against the traditional model of interesting challenges for the rich, versus mindless lockstep regurgitation for the poor. Of course, standards do not guarantee equity. The interpretation of the standards, the expectations of what students can accomplish, and the quality of teaching vary enormously whether under state or national standards, in a way that is usually linked to the socio-economic status of the students. That said, having common standards at least sets up a common framework and common goals, and can provide a helpful context to address these concerns and to compare different approaches.

Some Unconvincing Objections

Some people object to the Common Core as a one-size-fits-all curriculum, on the grounds that not everyone will pursue STEM (science, technology, engineering, math) careers. Of course, that's true, but not particularly relevant. For one thing, we should not proactively freeze some students out of those careers. If past experience is any guide, we can expect that would tend to limit STEM to well-off white boys. More fundamentally, the habits of mind outlined in the SMP are helpful for everyone, not just mathematicians, scientists, and engineers. They are in fact more useful to more students than any particular content standard, and they represent a broadening of the reach of what progressive educators have been calling for in the past 20 years. The SMP are largely a rephrasing of the NCTM Process Standards. This is an argument in favor of the CCSSM.

Some people claim that the Common Core is a plot of the publishers, because it will allow them to have a single version of a textbook, and sell it in every state. Frankly, if we can get thinner textbooks because publishers don't have to satisfy 50 different sets of standards, I think that's a good thing. (Math textbooks in other countries are much, much thinner than US textbooks, precisely because they have a national curriculum.) The real danger is not with the publishers implementing the CCSSM, but with the likelihood that they will not implement it, and slap on a “Common Core” sticker after only making superficial changes.

Some people object to the Common Core because in many locations, there are serious problems with the timing of the implementation. I agree with that concern, and discuss it below, but it does not invalidate the standards themselves, or their big-picture goals.

Some people claim the Common Core is part of a vast plan to privatize education. Certainly, public education is under attack, and that should be resisted. I will return to that in this paper, but I don't see the CCSSM as a necessary part of that assault, or opposition to the CCSSM as useful in resisting it. In my view, we should discuss the Common Core as an issue in math education and separate it from the important work that needs to be done in defense of public education.

Algebra

In algebra, the Common Core proposes a major shift in emphasis, from memorized symbol manipulation techniques to a balanced approach placing those techniques in the context of mathematical modeling. This is a long overdue change, and one that has already been implemented to different degrees in many of the curricula that were developed in the past 20 years.

For example, the word "simplify" occurs nowhere in the CCSSM. Understanding the concept of equivalent algebraic expressions is an important part of symbol sense, which can facilitate understanding and communication. But the mindless simplification of countless expressions with no rhyme or reason has been one of the ways we turn kids off to algebra and to mathematics in general. The same is true of endless factoring and equation-solving drills, when they are divorced from context or purpose.

A few students enjoy the routine aspect of those tasks, and those who are good at this sort of thing appreciate that they can get good grades without the anxiety they associate with problem solving. But for most, this kind of work is profoundly boring, and appears completely pointless. They are right to ask "When will I ever use this?", a question we can only answer lamely with mention of future tests and courses. The change in direction in algebra instruction proposed by the CCSSM redresses the balance: symbol manipulation is taught in tandem with modeling problems, which make direct reference to “real world” and other contexts (simplified as necessary) while asking students for intellectual engagement rather than mere regurgitation of memorized algorithms.

Alas, many teachers, parents, and students believe that rote memorization and endless repetition of such techniques is what math is. Well, they are wrong. There is a place for fluency in symbol manipulation, but given the existence of a wide range of technological tools, from calculators, to spreadsheets, to interactive geometry software, to powerful applets on the Web, that place is no longer the same as it once was. I do not claim to fully understand how to best combine and integrate technological, mental, and paper-pencil approaches, but I am confident that this is a question we need to ask ourselves. The claim that one or another of those approaches is the only one we need to teach is shallow and at the root of many problems in math education.

In fact, my own experience, and that of many others, is that a great reduction in the time spent on mindless paper-pencil manipulation, combined with intelligent use of technology in the context of mathematical modeling, is far more effective in engaging students, helping them develop the right habits of mind, and keeping them open to the possibility of taking more math and science classes.

Geometry

There are equally profound changes being proposed to geometry in grades 8-11. However, there is much less experience with the new approach. Instead of basing everything on congruence and similarity postulates, as is traditional, the idea is to build on a basis of geometric transformations: translation, rotation, reflection, and dilation.

Here is a pedagogical argument for the change: congruence postulates are pretty technical and far from self-evident to a beginner. In fact, many of us have long explained the basic idea of congruence by saying something like "if you can superpose two figures, they are congruent." That is not very far from saying "if you can move one figure to land exactly on top of the other, they are congruent." In other words getting at congruence on the basis of transformations is more intuitive than going in the other direction.

There are also mathematical arguments for the change: geometric transformations tie in nicely with such concepts as functions, composition of functions, inverse functions, symmetry, complex numbers, matrices, and basic group theory. Moreover, the traditional approaches to congruence and similarity leave a lot to be desired. If congruence is only clearly defined for segments, angles, and triangles, what about circles and arcs? If similarity is only defined for triangles and polygons, what about parabolas?

I have taught transformational geometry and its connections to a number of related topics in an elective course for high school juniors and seniors for more than 20 years, and I strongly support this aspect of the CCSSM. However we should acknowledge that much work needs to be done to develop a transformation-based curriculum that will work for grades 8-11. Because the change is fundamental, it may offer an opening for materials with more sophisticated pedagogy. On the other hand, the fact that it is so fundamental, and so unfamiliar to so many teachers, will probably make it quite challenging to implement.

Technology

The mention of "tools" in the SMP, and the various references to calculators, spreadsheets, computer algebra systems, and dynamic geometry software in the content standards is quite encouraging. The extent to which technology will be embraced, especially in those areas where the CCSSM fail to mention it, is an open question, but this is definitely a start, and an important one, which will support the changes in direction in both algebra and geometry. Where teachers and students can get access to computers and/or tablets, this is a good time for this change, as there are more and more free tech resources for math education. Moreover, the explicit mentions of technology in the CCSSM, and the use of tablets and computers for the assessments will almost certainly make it easier for schools to get funding for the needed hardware, as well as hopefully lead to a drop in prices.

A Historic Opportunity

Putting all this together, we can see that the CCSSM offer us a historic opportunity to make profound and badly needed changes to math education in the US. I intend to do what I can to help with this momentous project.

I wish I could end this paper here. Unfortunately, while I welcome any movement in this direction, I am not convinced that all of these good things will come to pass in the real world. Read on.

II. The Bad

Here are some reasons to be skeptical about the Common Core chances of success, and critical of its implementation and content.

Unrealistic Timetables

The CCSSM is being rolled out in a completely unrealistic timetable. It represents a profound change from tradition, and yet millions of teachers are expected to implement it immediately. This is a lot to ask, given:

- The scarcity of suitable curricular materials. Some excellent and some decent materials are being developed in a hurry, but how many teachers will they reach? And how likely that all of them will work well in their initial version? At this point, still early in the game, it seems like the textbooks used by most teachers are largely unchanged.

- The deep and widespread cultural obstacles to the SMP. Most teachers, parents, and students in the US believe that math education is the transmission of endless lists of techniques to memorize. They are wrong, but this cannot be changed by fiat. And unfortunately, while this approach is ineffective with most students, the people who become teachers tend to be the ones who did well under this regime, and therefore are not likely to see a need for change.

- The weak mathematical background of so many teachers, combined with the limited funding available to do anything about it. To take one example: I have a master's degree in mathematics from a prestigious university, and 42 years in the classroom, but I'll be honest: I don't understand many if not most of the statistics standards for high school. I could not realistically be expected to teach those effectively. Without significant further study, I would be pushed into teaching these standards superficially, relying on rote memorization and a use of technology that masks the underlying math, in direct contradiction to the SMP. More on this below.

Moreover, teachers will be expected to teach Common Core content and practices to students who have not experienced this approach in previous grades. Even if the teachers were ready, it will take some time to get students used to the new habits of mind implicit in the math practices, a very substantial change for many. Perhaps we don't need a full 13 years, following this year's Kindergarteners up the grades, but I don't see how this can be done in fewer than four or five years. And even that would require some support materials and a realistic strategy to ease the transition. As far as I know, those materials and that strategy do not exist at the scale that is required of a national initiative.

These are concerns that are not inherent to the CCSSM, but are about the expectations regarding its implementation. Many educators have spoken out about this, and the need to take it one step at a time has been acknowledged to different degrees in some school systems and publications. It is important for the authors and supporters of the CCSSM to be crystal-clear about the need for patience in implementation.

Alas, timing is not my only concern. The actual content of the standards is also problematic.

Geometry Shrinkage

The CCSSM continues what I believe is a long term trend in US math education: the gradual shrinking of geometry's place in the curriculum. This is not obvious from a superficial reading of the standards, because the CCSSM compensate for the disappearance of such topics as "the altitudes of a triangle meet in one point" or the properties of intersecting chords in a circle by dramatically increasing the amount of analytic geometry. In principle, I have nothing against analytic geometry, but when it's used to displace synthetic (non-analytic) geometry, we have a problem.

There was a time where geometry constituted about one-third of the three years of high school math that were required of college-intending students. In my view, that was too much, because teaching high school algebra effectively to the whole range of students does take an extraordinary amount of time. If, in addition, you want to include probability and statistics in the core sequence, as the authors of the CCSSM, and many math educators do, geometry cannot possibly fill up a whole year. But I can’t help feeling that geometry shrinkage has gone too far in the CCSSM.

My argument is not primarily about the teaching of proof, which I will return to later in this paper. It is about geometry as a subject. Geometry is the part of math where instead of breaking problems up into tiny pieces, we look at the whole picture, literally and figuratively. It is a part of math that appeals to a different type of student (and, frankly, a different type of teacher!) For many, it is the one part of math that "makes sense". For many, it is the part of math where the beauty of the subject is most apparent. It is the part of math where the connections to art and culture are the greatest. Simultaneously, it is the part of math where the connections to practical endeavors such as architecture, carpentry, and other building trades are the most obvious. In other words, teaching less geometry means reaching fewer students, and doing it less effectively.

Perhaps this shrinkage reflects the obsession with calculus as the end-all and be-all of secondary math education? Or is it simply evidence of the personal preferences of the writers of the CCSSM? In any case, it is a terrible mistake.

This development is particularly shocking because it is happening at a time where we can teach geometry far more effectively because of the advent of interactive geometry software. It is well known, by now, that this technology enhances learning in a variety of ways. Direct manipulation on a screen is an excellent environment to distinguish the essential properties of a figure from the particular way it appears on a static page. It makes it easy to generate conjectures, and to find counter-examples. It is what finally might help fulfill the promise of geometry as an appropriate arena for an introduction to proof. It is also a fine tool for teachers and curriculum developers to quickly create applets and microworlds to introduce powerful ideas. Finally, this technology is more accessible than ever, as it is now available with free software that will run on tablets as well as computers.

The decline of geometry cannot be justified mathematically or pedagogically. In fact, it could have, and should have gone the other way!

- 3D geometry could have been expanded. School math has long underemphasized solid geometry, a field with a very long history (Platonic and Archimedean solids,) beautiful results (Descartes’ theorem, Euler’s formula,) and multiple applications (chemistry, architecture, 3D printing.) This is another part of geometry made dramatically more accessible by technology. Absurdly, the CCSSM restricts 3D work to grades K-8. In high school, it appears only as a topic leading to the standard calculus problems.

- The CCSSM emphasis on geometric transformations could have provided a unique opportunity to expand the place of symmetry in the curriculum. Instead, symmetry as a topic is confined to elementary school, and to the analysis of Cartesian graphs, though it receives a passing mention in the high school geometry standards. The CCSSM could have been an opportunity to make connections with basic group theory and with such art-related topics as tessellations.

- Optional (+) topics could have included more advanced work with geometric transformations (for example: theorems about composition of isometries, connections with complex number arithmetic, a more complete coverage of transformation matrices, and some introductory work with geometric transformations in 3D.)

Perhaps you think that these suggestions merely reflect my own interests. Fair enough. For example, someone else might make an equally valid plea for the inclusion of binary arithmetic and other topics suitable to future computer scientists. (Or, in fact, to future citizens, given that computer science underlies so much of the world we live in.) But still, the shrinkage of geometry is objectionable for the reasons outlined above, irrespective of my own preferences.

Supporters of the Common Core point out that the standards that are listed in the document do not prevent one from teaching other things. Nothing could be further from the truth, for one simple reason: there are way, way too many standards, so the only way to teach something else is to not teach the full CCSSM, at an unknown cost in test scores, not to mention the veto that is sure to be wielded on such attempts by principals and school district bureaucrats.

Too Many Standards

Indeed, there are too many standards. I cannot prove this beyond the shadow of a doubt, but I know it is true because when I tried to fit them all into three years, based on my 32-year experience of what is a realistic program for grades 9-11, I could not do it. To teach all of the CCSSM well could easily take four years or more. To confirm my hunch I looked at a side-by-side comparison of the old California standards and the CCSSM for grades 9-12. It turns out that Common Core has 13 fewer standards than California used to have. As a fraction of the total, this is close to a difference of zero. Yet it is by now a well-established fact that no one could actually teach all the California standards in four years.

Or at least no one could teach them well. It is always possible to rush through as many topics as you want, as fast as you want, and then say that you "covered" the topics, when really all you covered was your ass. If not all students learned it, well, it's their fault! Having too many standards guarantees shallow coverage, less understanding, and plenty of opportunity to victimize teachers and students. If you want to teach a wide range of students effectively, you need to present important ideas in multiple representations: manipulative, symbolic, numerical, graphical, geometric, applied, technological. This is a standard feature of many of the better recent curricula, though in my opinion most do not go far enough in this direction, due to the time restrictions imposed by previous sets of standards.

Using multiple representations is important not only if you care about reaching different kinds of learners, whether the differences are due to personality types, educational background, or mathematical maturity. It also helps foster deeper understanding among those who might grasp techniques and ideas quickly. In other words, multiple representations are important both for access and for depth. They make it possible to engage the full range of students. It does take time to teach that way, but it is time well spent.

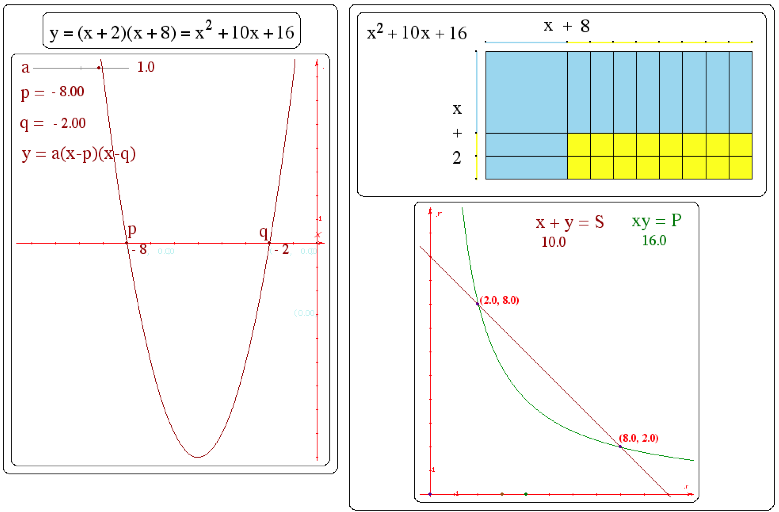
For example, here are five representations of the factoring of a trinomial:

	x	+2
x	x2	+2x
+8	+8x	+16

Introducing and discussing all of these representations is a lot more powerful both for access and depth than just looking at the first one. But having too many standards makes it impossible to do this.

Moreover, as mentioned above, having too many standards eliminates the possibility of including unlisted topics, whether as digressions from a standard curriculum, or in unorthodox electives. It also drastically reduces the opportunities to assign projects, go on field trips, use technology, and so on. In short, it is a pedagogical disaster, and it is in direct conflict with the SMP.

It is also one sure way to sabotage the transition to the CCSSM, since for at least a few years, teachers will need time to compensate for the fact that their students will not have seen previous-year CCSSM-mandated topics. The Common Core shoots itself in the foot.

Finally, having too many standards closes the door to innovation. If a curriculum is overfull, there is no space or time to try new ideas, whether they are pedagogical or curricular. Surely no one thinks the current version of the CCSSM is perfect as is, and moreover that it will retain its claim to correctness for ever. Yet, having this many standards makes it impossible to create something new while working with actual students. This would leave any future iterations of the CCSSM to a small number of PhDs who deem themselves able to divine what works without the benefit of actual classroom practice. That is not a recipe for success.

Only content that is truly foundational, the actual core understandings that make all others possible should be mandated, to make room for better teaching, for local flexibility, and for a wide range of electives in Year 4. An important conversation is needed to define such a core, and given the scope of the CCSSM, it is clear it has not happened. For example, it is not possible to do much further math without an understanding of the distributive law, or the Pythagorean theorem, or right triangle trigonometry. But do all students need to be able to explain that the sum of a rational number and an irrational number is irrational? I do not pretend to know where that boundary lies, but it must be drawn in such a way that there is realistically enough time to teach “really-core” standards well, while leaving an adequate amount of time for non-mandated topics.

Supporters of the CCSSM will argue that skipping the topics marked with a (+) makes the list more manageable. Obviously, there is some truth to this, but that is not going to be easy to implement, because familiar (+) topics will be hard to dislodge and replace with unfamiliar non-(+) topics. Moreover, some (+) standards have long been in the college preparatory sequence, and dropping those will tend to create a two-track system: the college prospects of students who have not been exposed to the (+) curriculum will almost certainly be worse than they are for the others. Finally, some states and districts will end up requiring these, for fear that omitting them would somehow imply low expectations (or, more nefariously, to use them as a way to sort students.) I will return to these questions below.

Too Much, Too Soon

Unfortunately, overabundance of standards is not the only problem. Another one is that the high school standards are poorly sequenced. At first, I was thrilled to hear that the CCSSM did not mandate a specific sequence of topics in high school, because in my view the traditional sequence is in part responsible for the many difficulties we have faced in secondary school math. My initial goal in studying the standards was to make some suggestions on a sequencing that is more likely to succeed. But that was before I learned that in fact, while a particular sequence is not required, two specific pathways are suggested. In the real world of public education, that is tantamount to a mandate, albeit one allowing two versions. I hope I will be proven wrong on this, but in all the cases I’ve heard about, districts and even entire states adopted one or the other pathway.

It appears that the only reason for the lack of a compulsory sequence is in order to strike a compromise between supporters of the traditional sequence and those who prefer an "integrated" sequence. The idea was almost certainly not to offer flexibility or room for experimentation or non-standard ideas, as I had naively imagined. (I should have realized that right away: there is no reason why the whole K-12 sequence could not have been organized in three- or four-year bands, as it was in the NCTM Principles and Standards.)

By the way, one piece of evidence about the fact that there are too many standards is that both pathways push some topics into a fourth year, even though the tests will be offered at the end of the third year. How this will play out in relation to tracking and acceleration is anyone's guess at this point. Tracking and acceleration are two practices that are at best debatable, and at worst harmful to many students. Both are tacitly endorsed in the CCSSM by the offering of "compacted" pathways that offer an accelerated program for grades 7-11. This is not at all surprising, given the relative power of the constituencies for and against tracking and acceleration in the current body politic. But it should at least lead the supporters of the CCSSM to reflect upon the overall impact of the standards as written. Will they end up being used to enshrine the current inequities?

In any case, I will share my thoughts about CCSSM high school sequencing. In the following, I assume that some students will start the high school sequence in eighth grade, so Year 1 means grade 8 or 9, Year 2 means grade 9 or 10, Year 3 means grade 10 or 11, and Year 4 means grade 11 or 12.

The Traditional Algebra 1 Course

For three decades as a math teacher and department chair, I tried to develop a curriculum and pedagogy that support the students who are not successful in traditional school mathematics, without harming those who are. In that time, I learned that the traditional Algebra 1 course is a crucial obstacle to equity. That course was initially designed for ninth graders. It was designed at a time when we knew much less about how children learn, and before the broad availability of technology changed the pedagogical options and the legitimate goals of algebra education. The course has changed from decade to decade, but some problematic features of it have survived over that time, mostly a very technical approach to symbol manipulation, largely divorced from meaning. This does not work well with the entire population of students in grades 7-9, nor is it compatible with the SMP and the new focus on modeling.

And yet, that course continues to be used as the gatekeeper for college preparatory math, and as a club to beat up students with shaky arithmetic skills — all the more so as it is being taught to younger and younger students. This is a national disgrace, and it cannot be pinned solely on the fans of "back to basics." Many progressive math educators bought into the illusion that requiring Algebra 1 for all, and Algebra 1 in middle school, would support their goals of equity in math education.

In fact, the opposite is true. Yes, middle school and Year 1 students can sing the quadratic formula. But the vast majority cannot understand it. They do not and cannot have the symbol sense required to have a feel for what it means, and they certainly cannot understand its derivation through symbol manipulation. As it turns out, one of the easiest and most powerful changes one can make to the traditional curriculum is to postpone extended work with quadratic equations and functions until Year 3. Likewise, solving equations involving absolute value or radicals, simplifying rational expressions, and any others among the highly technical Algebra 1 topics need to be saved for Years 3 and 4.

I know from experience that this delay makes it possible to teach these topics effectively to the vast majority of students, and in much greater depth. More importantly, it makes it possible to devote more time to important foundational algebra concepts in 8th and 9th grade, with an eye to understanding and sense-making. Early Algebra 1 is antithetical to algebra for all. Alas, few math educators understand this, and the CCSSM pathways do not support this idea.

Topics Best Postponed until Year 3

Suggesting that we delay some topics until they are accessible to most students may appear to be a push for lower standards. It is nothing of the sort. If students read Shakespeare in 9th grade, are they reaching a higher standard than if they study him in 11th grade? Quite the opposite: with a couple more years of maturation and schooling, they can understand Macbeth, say, in much greater depth. There is plenty of worthwhile literature that can be taught in 9th and 10th grade, to the benefit of all students. By the end of 12th grade, higher standards may well have been reached by postponing certain works. The same applies to math education.

Here are topics which should be reserved for Year 3, but appear in Year 1 or 2 of either the traditional or the integrated path. All of these topics can be previewed appropriately earlier than Year 3, but mastery should not be expected until the end of that year.

- Quadratic equations and functions, which should be taught in multiple representations, including the geometry of completing the square (for example as represented with algebra manipulatives) and the electronic graphing of parabolas.

- Function notation and related topics: there is no point in emphasizing terminology, abstraction, and notation before a concept is understood in practice. A good time to discuss function notation, composition of functions, inverse functions, and so on is after working with many functions in middle school and high school Years 1 and 2.

- Rational exponents: while some students can memorize the meaning and manipulation of rational exponents, teaching this prematurely is a waste of time, as it is sure to require repeated re-teaching. (I am only referring to interpreting and manipulating exponents such as ⅔. I completely support the teaching of exponential functions in Year 1, which obviously requires real number exponents.)

- Complex numbers: I disagree with the people who want to limit this topic to the mysterious introduction of i and its use in solving quadratics. The geometric interpretation is accessible and powerful both mathematically and pedagogically. It makes a beautiful final topic for students who will not be taking any more math, as it completes the process of expanding the student's experiences with numbers which started in Kindergarten. (And, incidentally, it’s a good way to review basic trig.) I see it as an end-of-Year-3 topic, and it should not be a (+) topic.

Topics Best Postponed until Year 4

Here are topics which should be reserved for Year 4, or omitted altogether from the Core. Of course, they would still be available for anyone to teach, if the overall list of standards were shorter. (See the discussion of optional topics below.)

Again, all of these topics can be previewed appropriately before Year 4, but mastery should not be expected until the end of Year 4. This is in part because of how challenging they are, but also tmoo create some breathing room in Years 1-3, so that the remaining standards have a fighting chance. Moreover, Year 4 is a time where students can reasonably be expected to decide on what makes a suitable elective math course for them.

- Polynomial, rational, and sinusoidal functions; radians; difficult trig identities. All these topics can be taught effectively in Year 4. Doing it earlier pushes them into rote territory. (Trigonometry can certainly be introduced in Years 2 and 3, both right triangle trig and unit circle trig. The basic graphs of the trig functions can be introduced in Year 3, as well as basic trig identities in the unit circle. But manipulating parameters that control periodic functions should be delayed until Year 4. Radians are not really needed until calculus. Proving complicated trig identities can be omitted altogether.)

- The binomial theorem: if you want evidence that this does not belong before Year 4, look no further than the footnote that suggests the theorem can be proved by using mathematical induction, a proof technique which appears nowhere else in the CCSSM. To be fair, it is also suggested it can be proved using combinatorics, which are in Year 2 as a (+) topic. But even on that basis, waiting for Year 4 would make it accessible to many more students. (Again, that does not rule out introducing parts of it less formally in previous years, for example with a coin-tossing random walk on an array of perpendicular streets.)

- Matrices: the best way to introduce matrices is on a foundation of transformational geometry and familiarity with the geometric interpretation of complex arithmetic. This makes it a great Year 4 topic.

- The remainder theorem is worthwhile for calculus students. A weaker version based on the zero product property is perfectly adequate for the Core.

- Rational and radical equations. Solving those “manually” is both difficult and boring and can be omitted altogether.

Additional Thoughts

Of course, I have not exhausted the issues that plague the content choices made by the authors of the CCSSM. Any close reading will generate questions reflecting the reader's priorities and beliefs. Here are a few more of my thoughts:

- Proof: The SMP emphasis on reasoning and argumentation provides a strong foundation for formal proof. Traditionally, an introduction to this is part of the geometry curriculum. In the CCSSM, that is maintained, and expanded to various algebraic topics. But if you think of mathematics as one of the humanities, as I do, you may object to the omission of indirect proof and proof by mathematical induction from the CCSSM. These ideas really belong in the culture of an educated adult, and should appear at least as a (+) option. They are much more interesting than some of the arcane and highly technical topics on the list.

- Statistics: Counting and introductory probability are excellent high school topics. But concepts in statistics such as linear regression, normal distribution, and standard deviation are based on assumptions and calculations that are not meaningful to most high school math teachers, let alone their students. Technology makes it easy to work with these concepts, but introducing them as black-box techniques is profoundly antithetical to the SMP emphasis on sense-making. If statistics is to be part of the math curriculum (as opposed to the science curriculum,) the variability of data can be discussed with the interquartile range, and line-fitting can be done with the median-median line. Such an approach gets to some of the same concepts in an intellectually honest way that is meaningful to both teacher and student.

In any case, choosing standards well is only part of the problem. Even legitimate standards can be counter-productive. If there are too many of them, or if they are introduced too early, access is reduced, and understanding is undermined. Unless something is done about this, we will see an expansion of a familiar problem, the one we encounter when the full dose of traditional Algebra 1 is pushed down the grades: a door slammed in the face of some students, and rote learning for the rest. Many will not be able to keep up with an unrealistic conceptual load. They, their teachers, or both, will get blamed.

III. The Ugly

The questions I raised in the previous section are related to developmental issues that cannot be wished away. Perhaps I am wrong about this, and my views only reflect the situation for students who grew up in a traditional program. Perhaps after growing up within the CCSSM, students will be able to manage the topics listed in the recommended pathways. If that is the case, one would hope that the tests will reflect the fact that it will take quite a few years for teachers and students to catch up with the CCSSM authors' vision.

Which brings us to the intimate connection between the CCSSM and high-stakes standardized testing. Assessment, of course, is an essential part of teaching. But the high-stakes tests which affect teacher retention and school survival consistently lead to bad teaching, as time and energy are wasted on the shallowest of test prep strategies, not to mention the pressure to cheat. Moreover, they force teachers to rush through each standard superficially, in order to say it's been "covered". This sort of teaching does not yield understanding, and is in fact in direct contradiction with the professed goals of the CCSSM.

Apparently, the new Common Core-aligned tests will be better indicators of understanding than their predecessors. If this is true, it would be excellent news, but then those tests should be put in the hands of the teachers, so they can use them to improve their practice. If they are used in the punitive way tests have been used since No Child Left Behind / Race to the Top, there is no chance for the Common Core to be successful.

I believe most of the groups and individuals who support the CCSSM know this. Why do they not speak up? Why can't they, for example, be on record on the profound contradiction between yearly high-stakes tests in grades 3-8 and the SMP? Why do they not call publicly for a reduction in the number of tests? For a way to do testing that furthers rather than undermine learning?

Thankfully this is less of a problem in high school, as (at least for now,) there will be a single test, near the end of 11th grade. But much damage will already have been done in grades 3-8.

IV. My Recommendations

Support the Goals of the CCSSM

Not enough geometry, too many standards, too much too soon... None of these shortcomings invalidate the goals of the CCSSM. If we can teach for understanding, if we can do more modeling and less symbol manipulation, if we can implement the SMP across the grades, if we can get past futile arguments between traditionalists and reformers, if we can use technology to free us to teach more interesting lessons, if we can have a more balanced definition of rigor — if we can do all that, math education will be vastly improved. The reason the Common Core is supported by many progressive educators is that they see all these possibilities. I agree, and intend to do what I can to help in my work as a curriculum developer and teacher trainer.

Prioritize Some Standards

Selecting priority standards needs to be an early discussion in every math department. Those standards are the ones that are foundational. Understanding them makes it easier to understand the others. They need to be taught well, by resorting to multiple learning tools and representations. They need to be previewed and reviewed, even if that means less time for the more arcane standards.

Introducing or expanding the place of transformational geometry and statistics will require a serious effort in both curriculum development and teacher training. But in other areas, the foundational topics are likely to be familiar, and there should be an abundance of support materials to teach those with a variety of approaches and avoid the idea that more time on a topic means spending more time looking at it the same way.

Sequence Based on Experience

Many teachers will not have the option to choose a sequence for the topics between years and within years. Those decisions have probably already been made in many districts and in some entire states. But any department that has that option should discuss sequencing based on actual classroom experience, and be open to tweaking it every year. Topics that are too abstract can be postponed. Topics that are more accessible because of technology can be taught earlier. Topics that are overloaded with content can be spread out. At least, that is the collaborative approach which allowed the math department I worked in for many years to develop an effective program.

As long as the endpoint is the same, paying attention to how students actually learn can only be a good thing. If that much flexibility is not available, I believe the integrated path is less problematic than the traditional path and would recommend that choice, largely because it delays some too-difficult Algebra 1 topics to Year 2.

Interpret the Standards

As educators, we have to commit to our actual students. Interpret the standards in whatever way makes most sense to you and your colleagues, and do not lose sight of your values. In particular, remember that the SMP should not be sacrificed to any particular content standard or to a mad race for "coverage", which is why they are listed over and over throughout the CCSSM documents.

Demand CCSSM v. 2.0

We need to make our voices heard about the content of the CCSSM. The NCTM has already come out in support of regular revisions to the Core, and we should support that. A version 2.0 needs to be developed, and we cannot let that happen without substantial input from actual teachers, and observation of how things play out in real classrooms. I have much respect for the academic heavies who deem themselves qualified to make those decisions on our behalf, but I’m sure they would agree that they are not omniscient.

The first and most desirable change, in my view, would be to reduce the number of mandated standards, and increase the number of (+) standards. If the required topics are limited to really core topics, there will be time for better teaching, which will mean actually higher standards, rather than only wished-for higher standards.

In addition, we could better serve a diverse population of students by offering a wider range of optional topics. For example: the ones I suggested above in the discussion of geometry; topics suitable for future computer scientists; an introduction to dynamical systems; fractals; the infinitude of primes; the uncountability of the real numbers; and so on. Such optional topics could be organized in strands that lead to different Year 4 elective math courses, so that Calculus would not be the only option.

Act Outside the Classroom

Implementing the CCSSM gives all of us an opportunity to grow professionally. Now is a good time to learn new approaches and to share our successes and challenges in teaching for understanding. This is most powerful when working with colleagues at each of our schools, but it's also a good time to attend conferences, surf the Web, and network with other educators.

But we should not stop there. We need to speak out as best we can against test mania and the broader attacks on public education. Math standards should be about helping students learn, not yet another way to attack teachers.

---------------------------------------------------------------------

My Blog | My Math Education Page | My Newsletter

To comment publicly, click here.

---------------------------------------------------------------------

Thanks to Amanda Cangelosi, Carlos Cabana, Jim King, John Hall, Lew Douglas, and Megan Taylor for their helpful feedback on earlier versions of this paper. The opinions expressed here are of course only my own.