Geometry of the Comics Section
I will start with a Calvin and Hobbes strip which poses an interesting question:

The challenge is to find AC if AC=2·AB and BC=5. As it turns out, there are many possibilities:
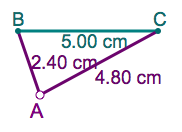
To find all of them, we can use interactive geometry software. Let us draw a circle with radius `r`, centered at B, and a circle of radius `2r`, centered at C. At their intersection, we have a point that satisfies the required constraint:
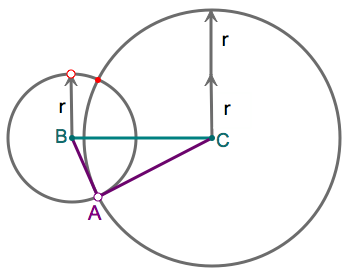
By changing the value of `r`, we can find all possible points A:
(Use the slider to change `r`. You can click on Trace and/or Locus.)
Download the GeoGebra file.
It appears that all the possible points A lie on a circle. The circle is called the locus of points A such that AC=2·AB. It can be found by using the "trace" or "locus" feature of the software. Of course, this does not constitute a proof, but it does provide us with a conjecture.
We can get the equation for the circle (and in fact prove it is a circle) by using the distance formula and doing some algebraic manipulation. A similar approach can be used to construct other conic sections, and to get their equations, thereby proving that the geometric definition is equivalent to the familiar algebraic one. This article will consist mostly of various approaches to the constructions, leaving the algebra for you to figure out.
Basic Constructions
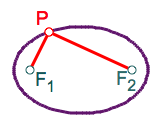
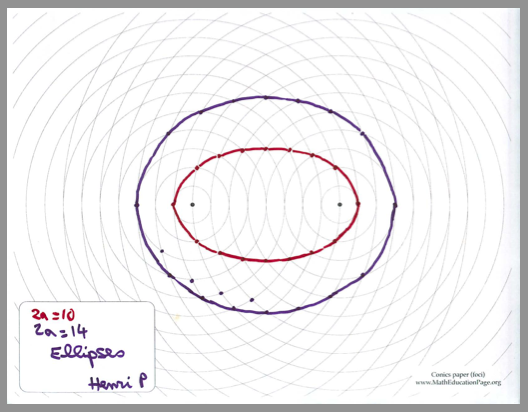
Definition:An ellipse is the set of points in the plane such that the sum of their distances to two given points (the foci) is constant.
In this figure, the radii of the two circles add up to a constant sum 2a. Thus, their intersections trace the path of an ellipse. (You can change 2a by dragging.)
(A similar construction is possible for the hyperbola.)
Low-tech alternative / prequel: Students can construct ellipses and hyperbolas "by hand", by applying the concept of the above construction on this conics paper. After choosing an appropriate value of 2a, they can find intersections of suitably chosen circles and mark those. Then, they can connect the marks. In fact, the low tech activity is good preparation for the computer approach, as it makes clear the idea behind the construction.
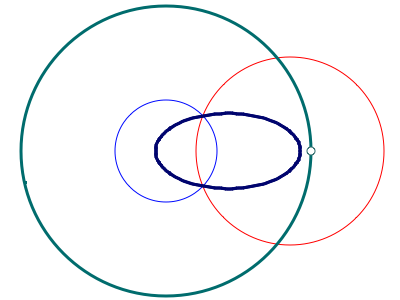
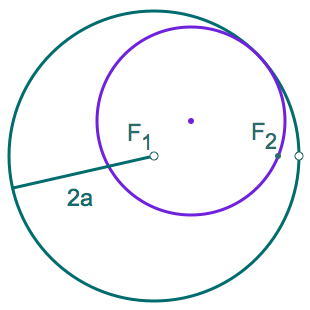
Another approach to the ellipse is based on the following construction challenge: given a circle with center F1, and a point F2 inside it, construct a circle that passes through F2, and is tangent to the given circle.
Connection: I used these Construction worksheets (Teachers' Notes) in Math 2, a version of Geometry. The activities therein should help develop a solid foundation for the mathematics on this page.
Here is a possible solution to the above challenge:
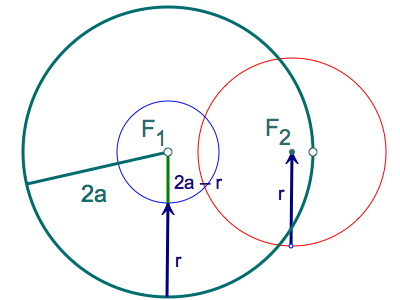
Let 2a be the radius of the original circle. Make a circle centered at F2 with radius r, and a circle centered at F1 with radius 2a - r. Either intersection of these circles can be the center of the circle we are trying to construct, since it is at the same distance r from F2 and from the original circle. For either of those points, the sum of the distances to F1 and F2 is 2a, a constant, thus the locus of the intersections is an ellipse:
(A similar construction is possible for the hyperbola, except that in that case F2 is outside the original circle.)
Focus/Directrix Definition
Another way to define the conic sections is with this single geometric definition: the set of points in the plane such that the ratio of their distance to a given point (the focus) to their distance from a given line (the directrix) is constant. The ratio is called the eccentricity of the conic.
If the eccentricity is 1, the distances are equal, and it's a parabola. If it is less than 1, it is an ellipse (a circle if it is 0.) If it is more than 1, it is a hyperbola.
This makes it possible to construct all three conics with a single construction.
The eccentricity is `r/s`, where `r` is the distance to the focus, and `s` the distance to the directrix. That ratio is set by the slope of the triangle on the left, which you can control by moving the visible vertex. For each value of `r` in the right-hand triangle, we obtain a value of `s` by drawing a parallel to the hypotenuse of the slope triangle, and finding its intersection with the directrix. We use a circle to get `s` onto a vertical line, which allows us to draw a horizontal line at a distance `s` from the directrix. We draw a circle of radius `r`, with the focus as its center. The two points where the horizontal line intersects the circle satisfy the condition `r/s=`eccentricity.
Low-tech alternative / prequel: Students can use the focus / directrix definition by applying the concept of the above construction on this focus/directrix paper.
Reflection Property
Here is a construction that reveals the reflection property of the ellipse:
Click the ► to animate.
Download the GeoGebra file.
The construction: The circle has radius `2a`. D is a generic point on the circle. Draw the diameter through D, and the perpendicular bisector of DF2. Call their intersection P. By construction, PD = PF2. Therefore for any D on the circle, PF1 + PF2 `= 2a`. Therefore the locus of P is an ellipse. (This is the most elegant of the constructions on this page, as it will create the locus in one piece. The previous ones were perhaps easier to understand, but they created the locus in two pieces, because they were based on circle intersections, which consist of two points.)
The reflection property: A ray of light originating at F1 will have an angle of incidence vertical to ∠DPM which, by construction, is equal to ∠MPF2. So ∠MPF2 is the angle of reflection, and the reflected light will go to F2.
A very similar construction and argument will work for the hyperbola, with F2 outside the original circle. (In fact, the above construction will create a hyperbola if you drag F2 out of the circle.) For the parabola, use a line (the directrix) in lieu of the original circle. (See this figure.)
An application of the reflection properties of both the parabola and hyperbola is the Cassegrain reflecting telescope:
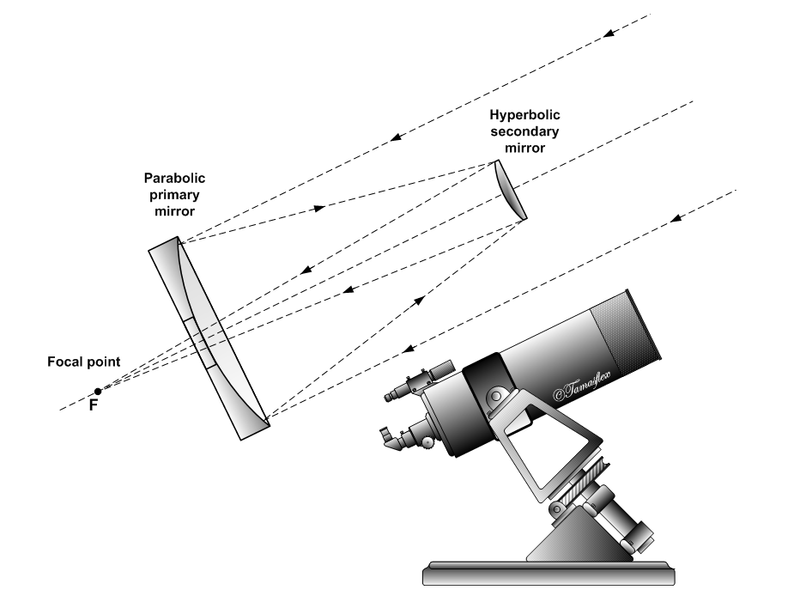
The light is reflected towards the focus of the primary parabolic mirror, which itself is one of the foci of the hyperbolic mirror. Thus, it is reflected by the secondary mirror towards the other focus of the hyperbola: the observer's eye.