A classic activity is to cover a 1-inch-side dodecagon with pattern blocks. This provides a great context to discuss symmetry (see Geometry Labs 5.6.) Here are two ways to do it:


A close look at these figures should help you find the area of the tan block. (The square has area 1 square inch.)
Pattern blocks can be divided into two families: on the one hand, the triangle and its multiples (blue, red, and yellow); and on the other hand orange and tan blocks. What makes the dodecagon tilings so beautiful and so fun to discover is that they combine blocks from the two families. You and your students should explore this! (It is easiest to do this using a pre-drawn outline, such as the one in Geometry Labs 5.6. See also this online applet: Symmetry with Pattern Blocks.)
Going Big
I've been a fan of the pattern block dodecagon for about forty years. In 2017, while thinking about something else, I stumbled upon a double-size, quadruple-area dodecagon. That launched me on a search for interesting tilings of that figure. Here are ten solutions I found:










I shared some of these on Twitter (where my handle is @hpicciotto), and it was not long before other pattern block buffs contributed some designs.
From Allendale, Michigan, John Golden:
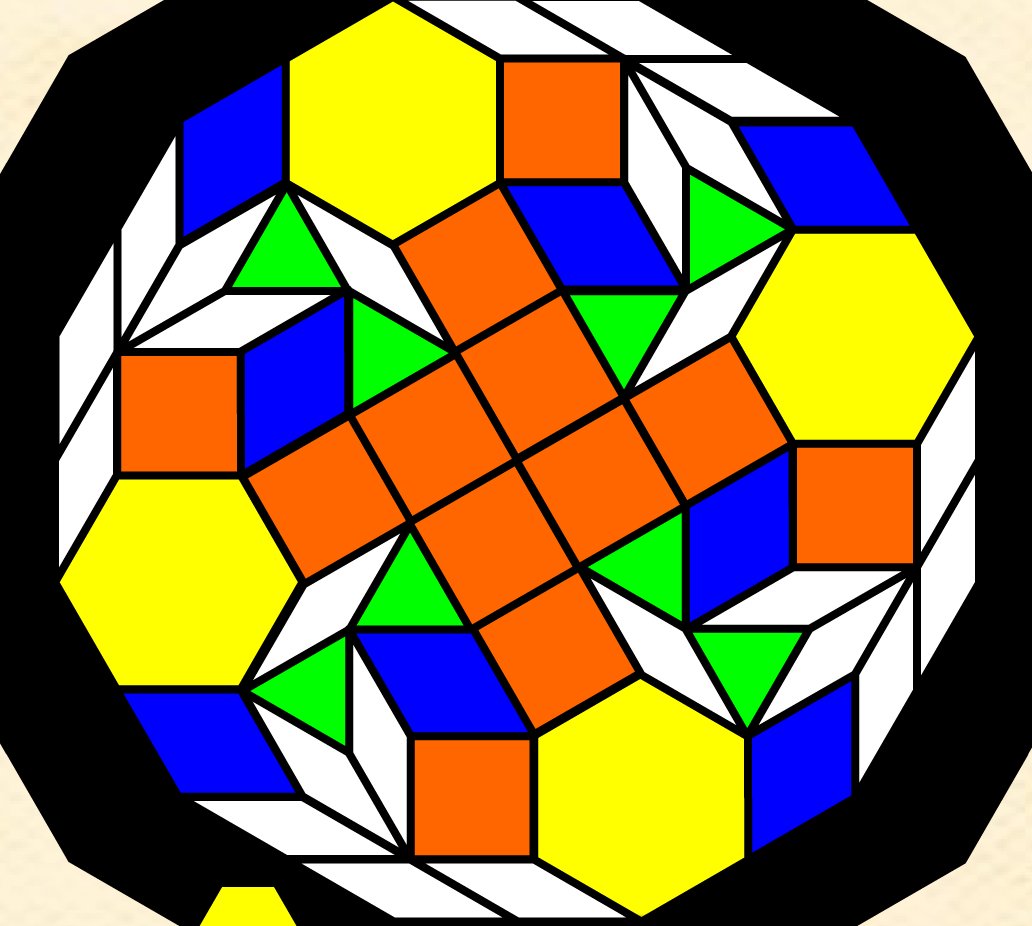
From Mallorca, Spain, Daniel Ruiz Aguilera:

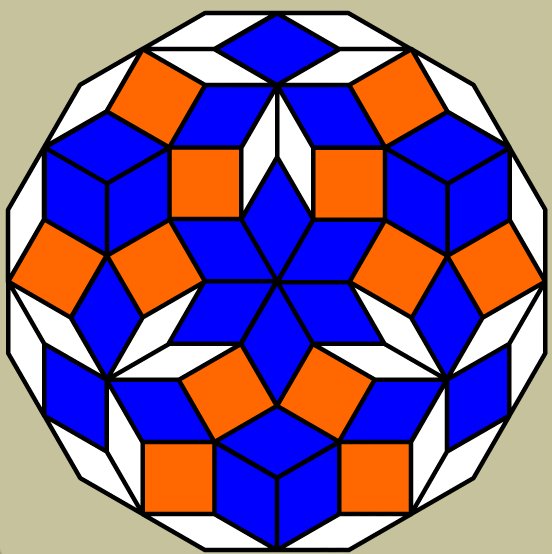
About the one on the right, Daniel asks: how many cubes do you see?
Notice that this next one has the same pattern as one of the dodecagons at the top of the page, with each of the blocks doubled. Since all the pattern blocks except the hexagon are rep-tiles, this method can be applied to any 1-inch-side dodecagons to create scaled versions of it, as long as it contains no yellow blocks. After doing this, one can do some substitutions to get aesthetically pleasing designs.

From Toulouse, France, Simon Gregg:





And these tripled dodecagons:


Simon found way to get bigger and bigger dodecagons by spiraling around:


From Strathcona County, AB, Hana Murray takes Simon's plan to the next level (side 4, and a mind-boggling side 10):


More side-2 designs:




Four sizes of the same basic design:

From Niagara, ON, Mark Chubb

From St Paul, MN, Christopher Danielson

And a quadrupled dodecagon by Christopher, implemented online by Mark:

You too, and your students, can play this game!
Download the dodecagon outlines, and get started!
Discussion
- Look for smaller dodecagons in the larger ones. In some cases, they overlap. Can you find a symmetric, but not regular dodecagon?
- One way to discover additional solutions to the larger dodecagon is to replace an internal regular side-1 dodecagon with a different one. (I do not share side-1 dodecagon solutions here, but I strongly encourage you to explore those. Many are beautiful.)
- In a given side-2 dodecagon, how many are there of each type of block? How did you count them?
- If the area of the square is 1, and the area of the triangle is T, what is the area of the dodecagon with side 1? side 2? side 3, 4, 10?
- If the area of the square is 1, what is T in terms of `sqrt(3)`? What are the dodecagon areas in terms of `sqrt(3)`?
- What combinations of blocks will work for a side-1 dodecagon? (Do not try to find all the combinations, but try to put in words, or in formulas, what must be true of the numbers of each type of blocks.)
- What symmetries are possible for a pattern block dodecagon? Are all of them represented on this page?
- Can you create pattern block dodecagons of your own for each type of symmetry? (Side 1? Side 2?)