Math Education Newsletter

A square lattice provides an excellent environment for rich activities. It is a microworld that students can explore on dot paper, or on geoboards. What makes it work so well is that it builds on student strengths: it is easier to look at discrete examples and whole numbers than continuous examples and rational or real numbers. If you are familiar with my books Algebra: Themes, Tools, Concepts and Geometry Labs, you know that I've used geoboards to introduce such topics as similarity, slope, area, distance, the Pythagorean theorem, and simplifying radicals. (Both books are free downloads on my Web site. I list the geoboard lessons and labs in this post.)

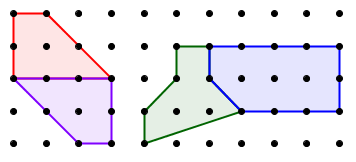
One particularly beautiful and surprising result in this context is Pick's formula, which gives the area of a geoboard polygon as a function of the number of pegs on its boundary, and the number of interior pegs. This result is can be discovered by students, in an activity which is both challenging and accessible. I link to worksheets on this, and provide a full proof of the formula (for teachers) on a new page in my Web site.

Finally, here are links to posts about two unsolved problems that are suitable for student exploration on the geoboard or dot paper:

No Three on a Line. (This one ties in with slope investigations.)

Heilbronn Triangle (This one connects with exploring geoboard area, or it can be used as an application of Pick's formula.)

I'll present more K-12 unsolved problems in future posts.

Functions are a major topic in the Common Core State Standards for math, starting in grade 8. This is quite a departure from traditional curricula, which postpone this topic until Algebra 2, in 10th or 11th grade. There's good and bad in this change.

＊ The good is that the concept of function is certainly accessible to 8th graders, and frankly even to elementary school students. An early introduction makes it easier to put algebra in context through modeling, and in fact can be a tool to teach many other things, including equations, inequalities, and even some important foundational ideas in arithmetic. This is not really a new idea: many curricula developed in the 90's did just that.

One such curriculum is Algebra: Themes, Tools, Concepts, a book I co-authored (more info and links to free download here.) A public school teacher in Utah wrote to me recently that he had been using the book with great success to teach the integrated path CCSSM Math 1. Read his comments here.

＊ The bad is that the authors of the CCSSM decided to introduce function notation too early in the game. Teaching this notation, as well as inverse functions and composition of functions is easy after students have had a couple of years of experience with the basic concept. Doing it in Algebra 1 is unnecessary, and only compounds the problems of that famously ineffective course.

I have a lot more to say on the Common Core. I will be posting my analysis on my Web site after I incorporate feedback from some friends and colleagues. Watch my blog for an announcement when the article becomes available.

Functions are important enough to deserve several representations: graphical, symbolic, numerical, contextual. To that list, I've added the parallel axes representation, or function diagram, a representation which makes many ideas about functions more accessible. For a general overview and many links click here.

Recent posts:

GeoGebra files for function diagrams: here and here

Function diagram applets

Function diagrams at the Asilomar conference and thereafter

Two fun talks I attended at Asilomar.

Thanks for reading!