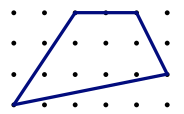
We will call simple polygons (no crossing, no holes) with vertices on lattice points geoboard polygons. Pick's formula for the area of a geoboard polygon is A = I + B/2 – 1, where A = area, I = interior lattice points, and B = boundary lattice points.
For example, in the figure above, the quadrilateral has I = 7; and B = 5, so the area should be 8.5.
You can confirm this is correct by subtracting the area of three right triangles from the area of the enclosing rectangle.
In the Classroom
Discovering this formula is within the reach of middle school or high school students, given a bit of guidance from the teacher. It is a beautiful and surprising result, which provides a wonderful connection between algebra and geometry, and it is both accessible and challenging in just the right way.
- Students can make the polygons on dot paper, or using rubber bands on geoboards. Good hints to support student exploration:
- - Start with small polygons.
- - Keep B or I constant, and see how changing the other affects the area.
- See also Lab 8.6 in Geometry Labs for a more guided discovery. In fact, that book contains much else for students to explore on geoboards and dot paper.
The Proof
The beginning of a full proof of Pick's formula may be appropriate for some students, but the rest of this page is mostly intended for teachers. All polygons mentioned are geoboard polygons.
The outline of the proof is as follows:
- The formula works for rectangles (horizontal-vertical sides.)
- The formula works for right triangles (horizontal-vertical legs.)
- If the formula works for two adjacent polygons, it works for the polygon they jointly create. And likewise if a polygon is removed from another, and both satisfy Pick's formula, then the remaining figure, if it is a polygon, will satisfy the formula.
- The formula works for any triangle.
- Finally, since the area of any geoboard polygon is the sum or difference of areas of triangles, the formula always works.
Rectangles
Here are two visual arguments to explain the formula in the case of a (non-tilted) rectangle.
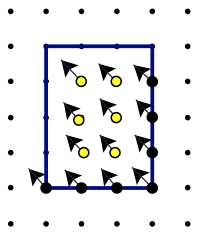
In this figure, each interior point and half the boundary points are matched with one square of area 1, the square immediately above and to the left of the point. It's almost a one-to-one pairing, but one of the squares lies outside the rectangle. Thus A = I + B/2 – 1.
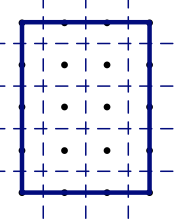
In this figure, each interior point is surrounded by a square of area 1. Each non-vertex boundary point contributes half a unit square. Each vertex contributes a quarter of a unit square. Adding it all up, we get:
`A = I + (B-4)/2 + 4(1/4)`
which is equivalent to the desired formula.
Right Triangles
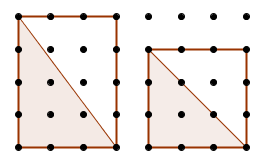
We will now prove that Pick's formula holds for right triangles whose legs are horizontal and vertical, like the ones in the figure above. The area of such a triangle is half the area of the enclosing rectangle.
Say that the rectangle's area is A, and it has I interior points, and B boundary points. Say that the triangle's hypotenuse passes through d of the rectangle's interior points, and that the triangle has i interior points, b boundary points, and area a. In the above examples, d=0 and d=2.
We have
and therefore:
But:Substituting the above values for I and B yields:
...which is what we were trying to prove.
Combining Areas
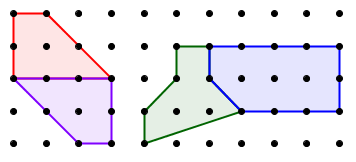
Next, we will prove that if two adjacent geoboard polygons satisfy Pick's formula, then the combined polygon, whose area is the sum of the two areas, also does.
Let us call the variables A, I, and B for the combined polygon, and a1, i1, b1, a2, i2, b2, for the two components. Finally, let us say the two polygons share S boundary points. (Note that to be able to combine the polygons into one, S must be at least 2. In the above examples, S=4 and S=3.)
We have:
But we are assuming the component pieces satisfy Pick's formula, so:
which can be rewritten as:
Just what we wanted! A similar argument can be used to conclude that if a compound geoboard polygon and one of the component polygons satisfy Pick's formula, then the other component polygon also does. (In other words, subtracting areas instead of adding them.)
It follows that any geoboard triangle will satisfy the formula, since any triangle can be obtained by subtracting right triangles from an enclosing rectangle:
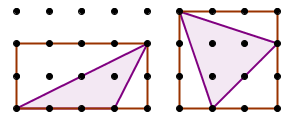
And since any geoboard polygon can be decomposed into geoboard triangles, we conclude that Pick's formula applies to all geoboard polygons. QED.
Reflection
Proof serves different purposes. One of them is to confirm something is true. Another is to help deepen one's understanding of the question under discussion.
I have been familiar with Pick's formula for decades, and have introduced it to many students and teachers. Still, I didn't feel I had a solid grasp of it until I saw the visual explanations of the rectangle case. Seeing those makes it crystal clear why the B term needs to be divided by 2, and what the -1 is about. So even though the rectangle case does not settle the matter, it is in some ways the most important part of the proof. It is the one part that seems worth thinking about presenting in the classroom, once the formula has been discovered by the students.
The rest of the proof is necessary to confirm the formula will always work, but it only adds a little to the gut-level understanding. Perhaps that is because those are more algebraic than visual? Still, it is satisfying to see how the algebraic manipulations work out.
That said, even though I am pleased with the proof, I don't think I'm done thinking about Pick's formula. Here is an interesting question that came up at our 2010 meeting.
Consider a triangle with a given base, and move the third vertex parallel to the base, as in this figure:
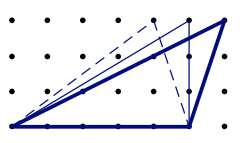
The area does not change, of course, but the number of interior and boundary points does. In the dashed triangle, I = 5 and B = 7. In the other two, I = 4 and B = 9. When we lost an interior point, we gained two boundary points. When we lost two boundary points in one place, we regained them elsewhere. But why? Pick's formula guarantees that will always happen, but that does not feel satisfying as an explanation. This is worthy of further exploration, reflection, and discussion with colleagues, and perhaps with students.