Hello,
If it weren't for COVID-19, I would have been out demonstrating in support of black lives, and for a redirection of resources from police to health and education. But I'm 70 and pre-diabetic, so I haven't been out much in the past couple of months. On the positive side, that's allowed me to pursue some long-delayed website projects and blog posts. (See below!)
Another consequence of the pandemic is that the two instances of my summer workshop on Hands-On Geometry (for grades 6-8) are being converted to online courses, as part of summer and fall math institutes. I expect I'll learn a lot about distance learning! Scroll down for more information.

Blog Posts
Here are links to posts on my Math Education Blog that you might find interesting.
If you are so moved, you may comment on the posts, and/or subscribe to the blog.
There Is No One Way
Frequently asked question: doesn’t using multiple approaches to a topic confuse the students? Well, yes, it may. It is especially confusing when connections are not made between the approaches, or when the teacher’s understanding of an approach is superficial. But we run greater risks if using a single approach. Multiple representations do not just make for better teaching. They are dictated by the math itself. This is what I discuss in this post.
User-Controlled GeoGebra Animations
This is a step-by-step tutorial on how to create those. I prefer to leave the control of the animation in the hands of the user: it allows them to think about the figure at their own pace, and backtrack if needed, rather than passively watch a video. It also makes it easier for a teacher to lead a discussion of the figure, step by step, while projecting it on a screen. (To see applications of this approach, check out my GeoGebra applets.)
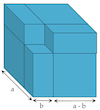
Sum and Difference of Cubes
The formulas for factoring the sum and difference of cubes are not a huge priority in high school math, but if you teach them, you might be interested in how they can be proved visually with the help of the Lab Gear. Read about this here. (This argument does not appear in the Lab Gear books.)
MathEducation.page
New on my Web site.
Lab Gear Drawings
Speaking of Lab Gear... I created Virtual Lab Gear: Google Drawings that teachers and students can use to make Lab Gear graphics. They may be useful for remote learning and collaboration, for presentations, to include in other documents, for homework or reports — and who knows what else. Figures can be annotated with text, and multiple people can work on the images at the same time.
Symmetry
Symmetry is an important topic in mathematics, but it is not explored much in school. This is unfortunate, because it is of interest to many students, and provides many "real world" connections to art and culture. I set up a Symmetry home page on my site, with links to the symmetry materials I've developed over the years, including some recent creations (1st grade to adult!)
Wallpapers Catalog
From the point of view of symmetry, there are exactly 17 ways to create a repeating two-dimensional design. I made a catalog of such designs, with each mathematically different design represented using pattern blocks. Katherine Paur and Simon Gregg contributed their creations to the catalog.
I analyzed one wallpaper pattern in depth in these blog posts: Part 1 | Part 2.
Not unrelated: I added some contributions from other educators to my Pattern Block Dodecagons page.
