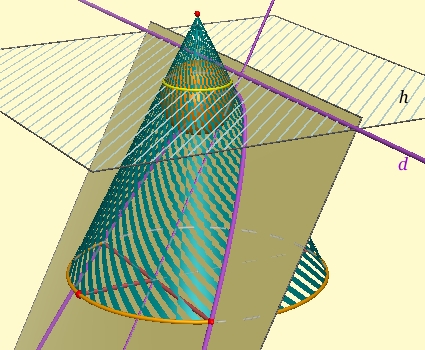
If you slice a cone with a plane that is parallel to a line on the cone through its vertex (such as UV on this figure), the intersection is a parabola. Here is a proof of this fact.
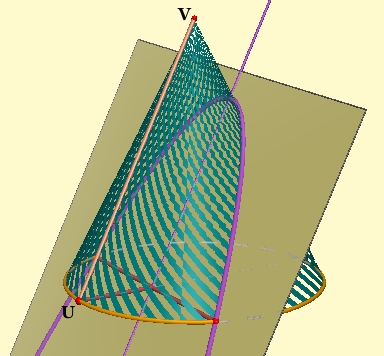
Construct a sphere that is tangent to the cone and to the plane. (Its center is on the cone's axis, and on the line halfway between the plane and UV. Its radius is half the distance between UV and the plane.)
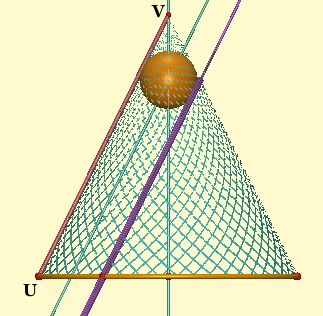
The sphere touches the cone along a circle (yellow in the figure), and the plane on a point (F in the figure.)
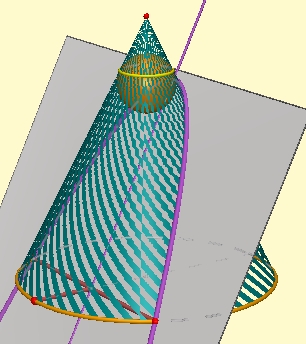
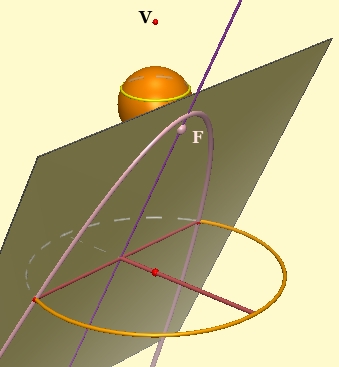
The circle's plane (h) intersects the original plane in a line (d in the figure.)
We would like to show that all points on the cone-plane intersection are equidistant from F and d. Let us choose a generic point P on the intersection.
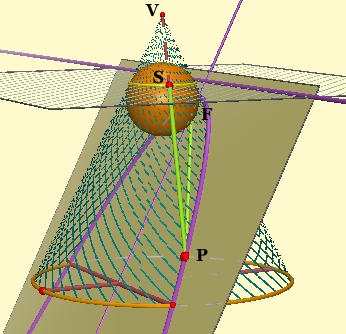
S is the intersection of PV with h. PF = PS, because they are both tangents to the sphere from P.
PT is the perpendicular from P to d. PR is the perpendicular from P to h. We want to show that PT = PS. To do that, we will show that right triangles PRS and PRT are congruent. Since they share leg PR, it is sufficient to show that angles TPR and SPR are equal.
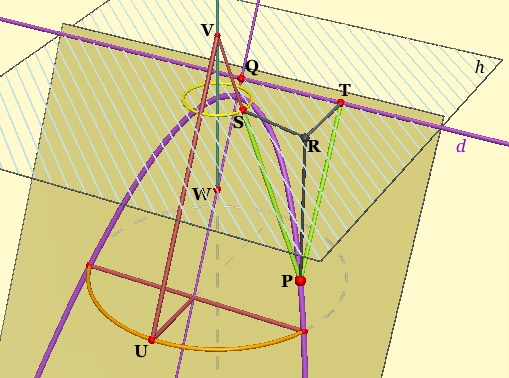
VW is the cone's axis of symmetry. Notice that angle SPR is equal to angle SVW (VW and RP are parallel, and the angles are alternate interior.) Angle TPR's sides are parallel to those of angle QWV, which is equal to angle WVU (alternate interior, with parallels QW and UV.) Since angles SVW and WVU are equal, being half of the cone's vertex angle, it follows that angles TPR and SPR are equal, our triangles are congruent, and thus PT = PS.
Finally, since PT and PF are each equal to PS, they are equal to each other, which means that P is equidistant from F and d. Thus the intersection of the cone and this plane is indeed a parabola. QED