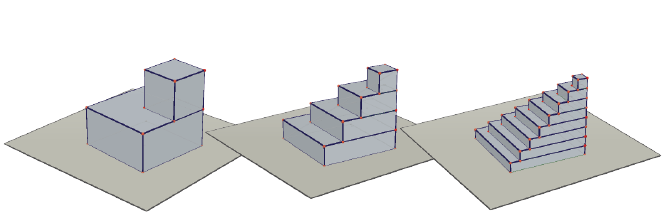
Let's start by finding the area under y=x2 from 0 to b, with interval length 1, using right-hand summing. This is equivalent to summing the squares of integers in the interval (0,b).

On the top of the left picture are numbers 1-4, represented by length. Below them are their squares. On the bottom of the left picture and more clearly shown in the right picture are the sums of those squares.

These pictures show what the shape approaches as the interval goes to 0 and n goes to infinity. Here I switch to Cabri 3D as the Urban School doesn't have the budget for infinite plastic blocks, nor do I have the time:
Here is the limit of the solid as n goes to infinity, a pyramid:
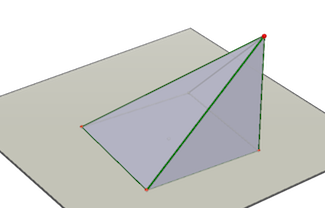
This one-minute movie shows that three of these pyramids exactly fill a cube:
Therefore the area under the graph of y=x2 between 0 and b is b3/3.
QED