The Glide Reflection

Space is a course I taught from 1991 to my retirement from the classroom in 2013. It included a fair amount about transformational geometry, a part of math which at the time was a somewhat eccentric preoccupation of mine. But the Common Core State Standards for Math (CCSSM) pushed the topic into the mainstream, more or less, a development I welcome.

On this page, I explain the significance and importance of the glide reflection, an important rigid motion that is not mentioned in the CCSSM.

The CCSSM mention three rigid motions (aka isometries), and suggest some basic assumptions about them. The three are reflections, translations, and rotations, and they are indeed fundamental. This post is about a fourth isometry, the glide reflection. I do not think it would have made sense to include it in the CCSSM, because those standards are already overstuffed. (See my analysis here.) Quite the opposite: in an ideal world (ha!) the CCSSM would be pruned so as to really consist of core standards only. In such a world, there would be time to teach actually-core standards well, and to complement them with interesting mathematical side trips. Of course, the side trips would not be the same in every school or every classroom.

Glide reflections belong in such an ideal-world side trip. In the less-than-ideal world we live in, they can provide some good exercises and problems in grades 8-10, serve as an enrichment topic in precalculus, or be part of a full-fledged unit in a Year 4 advanced geometry elective.

But enough introduction.

A glide reflection is the composition of a reflection, and a translation in a vector parallel to the line of reflection. This image gets the idea across:

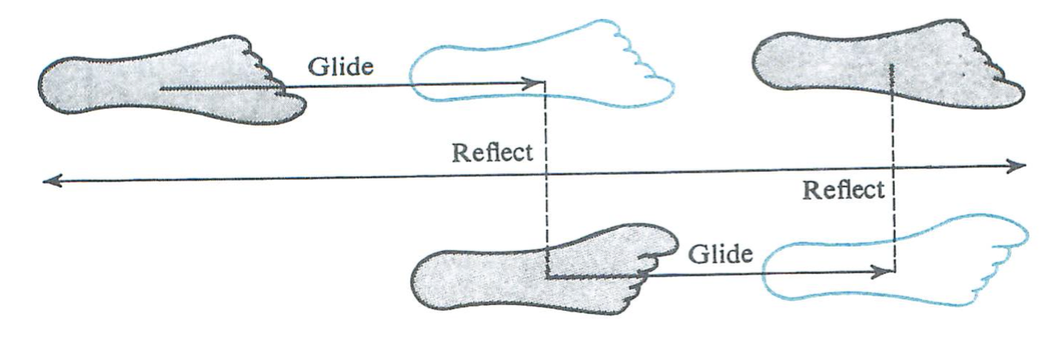
(The figure is from Richard Brown's excellent but dated and out-of-print Transformational Geometry)

And here is an interactive figure:

Of all the possible compositions of isometries, it may seem like a completely arbitrary choice. For example, why not give a special name to the composition of a reflection and a rotation? or a reflection and a translation whose vector is perpendicular to the line of reflection? I am glad you ask these questions. I offer three arguments for the unique significance of the glide reflection:

#2 is truly a fundamental and phenomenal theorem. Think about it: in the CCSSM, two figures are deemed congruent if one is the image of the other in "a sequence of rotations, reflections, and translations". What this theorem tells us is that if there is such a sequence, then it is equal to a single rotation, reflection, translation, or glide reflection.

See the epic proof of this result, abundantly and interactively illustrated with the help of GeoGebra, here. (Along the way, we prove #1.)

As one way to experience this at an intuitive level, you can have your students guess the mystery isometry, in various cases, starting here. The "cheat" button will likely not be necessary, but it is there just in case. Note that the activity is more fun if you go a little further: if it's a reflection, where is the mirror line? If it's a rotation, where is the center? (The latter question is hard for most beginners.) Note that reflections and translations require a fairly special setup, while rotations and glide reflections are very general. From the point of view of congruent figures, one can argue that glide reflections are as important as rotations.

As for #3: what do I mean by symmetries beyond the rosette? In fact, what do I mean by rosette, frieze, and wallpaper symmetry? Read on.

Here is an additional argument in defense of the glide reflection: its importance in analyzing symmetric figures. The Common Core does not have much to say about symmetry (see my analysis.) This is unfortunate, because symmetry provides us with connections to art and design, as well as to abstract algebra, and is very interesting to students.

Symmetry is deeply connected to rigid transformations, and can be defined in terms of those: a figure is symmetric if it is invariant under an isometry. (In other words, if it is its own image in an isometry.) In the most familiar example, bilateral symmetry, the isometry in question is a line reflection. Another well-known symmetry is rotational symmetry. In these examples (from my Geometry Labs), the stick figure is its own reflection in the red line, and the recycling symbol is its own image in a 120° rotation around its center:

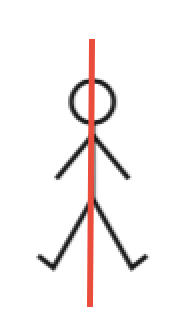
Therefore the stick figure is line symmetric, and the recycling symbol is rotationally symmetric. These are example of symmetries for finite figures. They are known as rosette symmetries.

But what if we have a figure that is its own image under a translation? That is the case for this infinite row (or frieze) of evenly spaced L's. It is its own image under a translation to the left or to the right by a whole number of spaces:

... L L L L L L L L L L L L ...

A frieze can be thought of as an infinitely wide rectangle, with a repeating pattern. A symmetry group is the set of isometries that keep a figure invariant. As it turns out, there are only seven possible frieze symmetry groups. In the example above, translation is the only isometry that keeps the group unchanged. But look at this one:

It is invariant under the composition of a horizontal translation and a reflection in a horizontal mirror. In other words, a glide reflection. If you want to analyze frieze symmetry, the glide reflection is absolutely necessary.

Likewise, if you want to analyze wallpaper symmetry. In this Escher design, for example, the light-colored birds are images of the dark ones in a glide reflection (the reflection lines and translation vectors are vertical.)

Do all students need to know this? Probably not. But to some of us, this is a lot more interesting than many of the "real world" applications of math we have the opportunity to think about.