"Super-scientific notation" is a phrase I coined to describe the process I use to introduce base 10 logarithms. The approach assumes that students are familiar with scientific notation, and already know how to use graphing technology to solve equations. In particular, they should be able to solve an equation of the type `10^x=1200` that way. (See #1-3 on the worksheet.)
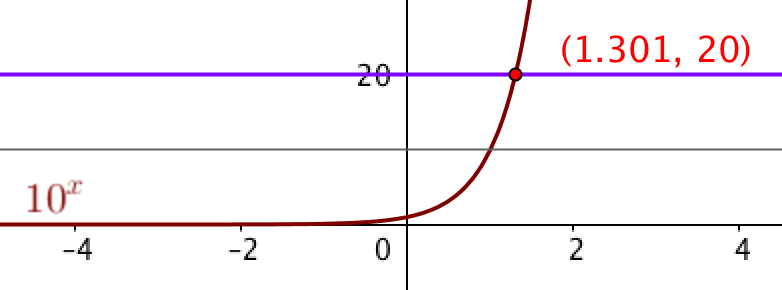
If you are using Desmos or GeoGebra, help students get started by demonstrating how to find the intersection of `y=10^x` and, for example, `y=20`. Here is a GeoGebra file you can use to facilitate further discussion.
If your students are using a TI calculator, you may print out these TI-83 calculator screen shots, and make a handout or transparency out of them. Note that the window is set correctly by first observing that x is between 3 and 4, since 1200 is between `10^3` and `10^4`.
If your students have access to CAS software, and just push a "solve" button, you should consider giving them a filled-out chart after they find a few values on their own. Finding the numbers by graphing is worth doing, because it forces some thinking about where the intersection will be. Finding them with CAS, not so much. In any case, it is OK for the students to share the work in filling out the chart, as the patterns often trigger worthwhile conversations.
As they work through the activity, students become aware of the fundamental properties of logarithms, in their form as properties of exponents. I do not mention the word "logarithm" until this activity has been completed and thoroughly discussed. This is almost certainly not on the same day as the students complete the activity.
Interestingly, while at the end of the activity there is fairly good understanding of the fundamental structure underlying logarithms, and how to use it, much of that understanding is still fragile, and students typically suffer a setback once the word "logarithm" and the accompanying notation are introduced. However the concept of super-scientific notation remains a solid foundation that you can refer to when students are confused.