Also using the Circle-Trig Geoboard: Angles
An introduction to logarithms that likewise postpones terminology and notation until after the concept has been introduced: Super-Scientific Notation.
© Some rights reserved
https://www.mathed.page/circle
Henri Picciotto's Math Education Page
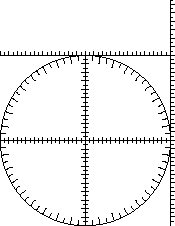
An introduction to the trigonometric ratios
by Henri Picciotto
These activities are adapted from my book Geometry Labs. They provide a new entry into trigonometry. You can use them as a preview / introduction to trig, in grades 8-10; or as a complement to a traditional or electronic-based approach, in grades 10-11.
See the teacher notes below for sequencing suggestions.

(For more lessons from Geometry Labs, see Angles on this website, or just download the whole book or part of it for any non-commercial use.)
Of course, the activities are far from offering a comprehensive coverage of trigonometry, but they do introduce the basics of right triangle trig, plus the unit circle, in a way that should be accessible to just about all students.
The essential tool for these activities is the 10-cm-radius circle, which includes:
The ten-centimeter circle is available as the CircleTrig Geoboard, from Nasco, or in a paper version which you can duplicate for your students. Download one or more of these:
Or find a hard copy in Geometry Labs. Depending on which original you use, and the properties of your printer, you may need to use your copy machine to adjust the size so that the radius is really 10 centimeters. (This is not strictly necessary, as it is possible to just use the built-in rulers, so consistency with actual centimeter measurements is not required.)
Acknowledgments: I was inspired to develop this approach by Sherman Stein, Cal Crabill, and Don Chakerian's Trigonometry.
The activities start with an introduction to the tangent ratio, which is more accessible than sine and cosine and is related to the already familiar concept of slope. In the book, the sine and cosine ratios follow. (I introduced the tangent ratio in the first semester of Geometry, and the sine and cosine in the second. Separating them that way increases student exposure to the concepts, offers an opportunity to review, and focuses on the concepts rather than on mnemonics.)
It is best to start by introducing the concept of "slope angles" and the 10-cm circle to solve standard right-triangle trig word problems, such as the ones in Lab 11.2. This establishes the motivation for filling out the tables in Lab 11.1. Or perhaps solve a few of the problems in 11.2, then do Lab 11.1, and finally do the rest of Lab 11.2. (Likewise, I recommend tackling Lab 11.5 before filling out the tables in 11.4.)
The words "tangent", "sine", and "cosine" are not used right away, mostly as a way to keep the focus on the geometric and mathematical content. Of course, these names need to be introduced sooner or later, and you will have to use your judgment as to whether to do that earlier than is suggested here. If you are using these labs in conjunction with other trig lessons, you may not have the option of postponing the introduction of the names, given that students will recognize the ratios.
In any case, when you do introduce the names, you will need to address the students' question "why are we doing this when we can get the answer on the calculator?" For me, this answer has worked: "you can use your calculator if you want, but for these first few activities, show me and show yourself that you understand the geometric basis of these ideas". The calculator is the method of choice if you're looking for efficiency, of course, but the geometric representation in the circle is a powerful mental image, which will help students understand and remember the meaning of the basic trig functions. Making the tables is also a way to explain how trig tables were used to solve these problems before the advent of calculators.
The ten-centimeter circle is a flexible tool in the introduction of trigonometry, and of course can be used to solve right-triangle trig problems from any source. You will no doubt find your own uses for it. To get you started, I include the first two activities here -- more are available in the book, in a ready-to-duplicate format.
Print and duplicate "Slope Angles". (This is Lab 11.1 in Geometry Labs.)
Prerequisites: The concept of slope. The concept of similarity.
Teacher's Notes: This is an introduction to the tangent ratio, and to the arctangent. You should probably demonstrate the correct procedure (as shown in the figures). It is possible to get a reading accurate to the nearest degree or millimeter, so the tables can be accurate to two significant digits.
Print and duplicate "Using Slope Angles". (This is Lab 11.2 in Geometry Labs.)
Prerequisite: "Slope Angles".
Teacher's Notes: This lab provides applications for the work in the previous lab. The last two questions open up the issue of interpolating and extrapolating, since the tables we made then were clearly insufficient to deal with the full range of problems of this type.
In doing this work, it is helpful to orient the figures so that the rise is vertical, the run is horizontal, and you are dealing with positive slopes only. Eventually, when the tangent ratio is officially introduced, the formulation "opposite over adjacent" will be more flexible, as it can be applied to a right triangle in any position.
After doing these activities, you can pursue any or all of the following options if you want to do more work on this topic:
Related pages on this site:
Also using the Circle-Trig Geoboard: Angles
An introduction to logarithms that likewise postpones terminology and notation until after the concept has been introduced: Super-Scientific Notation.