Fraction Arithmetic on Grid Paper:
The Well-Chosen Rectangle

This is an introduction to a visual approach for fraction arithmetic, using an area model on grid paper. It should not replace other approaches: it can complement them, or precede them, or follow them. I do not propose this as a way to get students to be quick and accurate in their calculations. Rather, it is an attempt to have them develop some understanding. The teacher's role is crucial in making connections to other approaches.

My goal here is to offer students

• an approach that is hard to forget — as opposed to multiple techniques that are hard to remember
• a visual representation of the fractions themselves, and of the four operations, providing a foundation for conceptual understanding
• a context for reflection and discussion, both among students, and in whole-class conversations led by the teacher

I share this approach in short homemade videos (6 to 10 minutes each), and in text. You can choose your preferred format, but I encourage you to use both, as they emphasize different aspects of the issue under discussion. (In fact, for division they present different strategies.)

I apologize for the questionable quality of the videos: I'm new to this medium.

Note: In the videos, I hand-draw the rectangles on grid paper. This is because that's how I expect students to do it. On the other hand, you may find the Fraction Rectangles applets convenient when demonstrating the ideas remotely or when using a projector in the classroom. In fact, there is no reason to not let students use the applets themselves if your tech setup allows it. (The applets are just a shortcut to creating the figures, they do not do any actual arithmetic.)

There are many ways to represent fractions: on a number line, in a "pie", in a rectangle, and no doubt others. Each representation is useful and important, and it is a mistake to limit oneself to just one. This page is about using rectangles on grid paper, an approach I discovered back in the 1970's when I taught 4th and 5th grade.

The key idea is that if I want to look at `3/4`, say, I'll represent 1 using a rectangle with length or width equal to 4 (the denominator of the fraction). The other dimension does not matter, and can be whatever is convenient for the problem at hand. Whatever that other dimension is, the rectangle can conveniently be divided into fourths, and thus be used to help represent `3/4`.

Note that of course I can represent `3/4` as part of a line segment, which is really the underlying reason this works on the rectangles. But it is the rectangles which will be most useful from here on out.

Trying to decide which of two fractions is greater (perhaps to place them on a number line?) is not always easy. It is made much easier by the use of well-chosen rectangles.

For example, which is greater, `2/3` or `3/5`? We'll use 3 by 5 rectangles to figure it out:

Those dimensions make it easy to represent each fraction in its own rectangle. We can readily see that `2/3` consists of 10 grid squares, while `3/5` consists of 9. Therefore, `2/3 > 3/5`.

But what does a grid square correspond to in this situation? Remember that each rectangle represents one unit, or 1. Each rectangle is divided into 15 squares. Therefore, each square represents `1/15`, and our two fractions are `10/15` and `9/15`. 15 is a common denominator.

Comparisons like this one can eventually lead to fruitful discussions. How would we answer this question without the rectangles?

We follow much the same strategy to add and subtract.

Let's say we want to add `2/3` and `1/5`. We will use grid paper to make it easier to visualize what is going on. If one unit was defined as a 3 by 5 rectangle, we could easily represent either fraction in it:

But now we see that the sum has to be `13/15`.

The same figure helps us see that the difference has to be `7/15`.

The key is to have students decide on the appropriate rectangle for a given sum or difference. What is it about a 3 by 5 rectangle that made it useful for this situation?

For multiplication, once again, we choose the rectangle with the most convenient dimensions, but this time we use the area model.

Let's say we'd like to multiply `2/3` by `1/5`. This time, we will represent these fractions one-dimensionally, using line segments on the sides of the rectangle. Again, a 3 by 5 rectangle will come in handy:

The product will be the area of the subrectangle with those dimensions, in this case it is `2/15`. This method would still work for fractions greater than 1. Here is `4/3` times `1/5`:

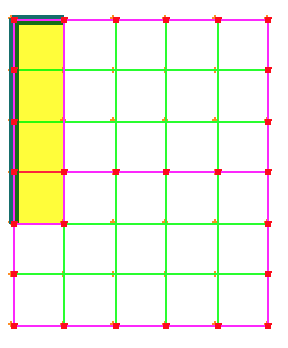
It is of course important to remember that each rectangle is one unit, so that the answer here is `4/15`.

Unsurprisingly, division is more difficult. I present two strategies. In the video I share an approach which is probably the more accessible of the two, as it is largely based on what we've done with the other operations.

In the rest of this section, I share an approach which is more challenging, but perhaps offers greater insight. The idea is to observe what happens when using the area model to divide by smaller and smaller numbers.

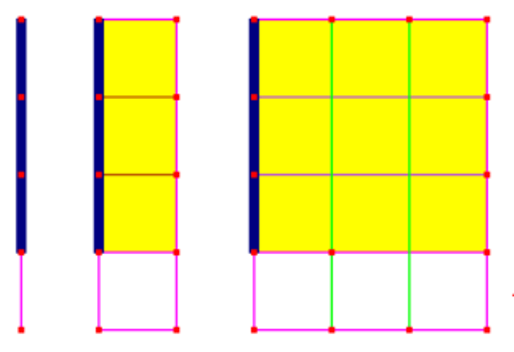
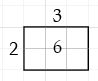
We will arrange the divisions in a manner similar to the layout for long division. For example, 6 divided by 2 equals 3 would look like this, with 6 as the area of the rectangle, the divisor 2 as the height, and the quotient 3 as the width:

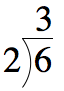
All the rectangles on the rest of this page have area 6. These represent 6 divided by 6, 3, 2, and 1:

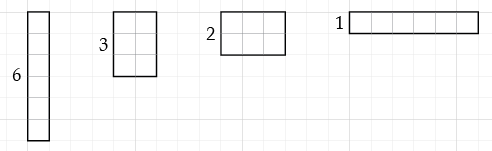
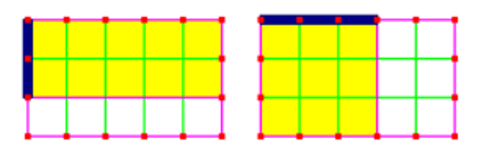
As the divisor gets smaller, the quotient gets bigger. (In fact, when we divide the divisor by n, we multiply the quotient by n.) Continuing that process, we represent the division of 6 by 1, `1/2`, and `1/3`:

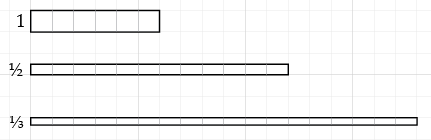
In order for the area to still be 6, we see that when we divide 6 by `1/n`, the quotient must be 6 times n. (To divide by a unit fraction, we multiply by its reciprocal.)

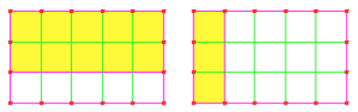
But what if we are dividing by, say, `2/3`? Since we are multiplying the divisor by 2 (as compared to 6 divided by `1/3`,) we have to divide the quotient by 2:

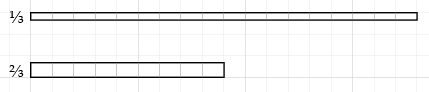
So to divide 6 by `m/n`, we multiplied by n, and divided by m, which amounts to multiplying by `n/m`.

In short: to divide by a fraction, we multiply by its reciprocal.

The grid paper approach does not cover every single fractions concept. For example, I have not found a straightforward way to address the idea of least common denominator or lowest terms within it. Still, it is a flexible and powerful tool:

• The central idea is straightforward: choosing a rectangle with the most useful dimensions. That one big idea is used repeatedly to do many different things.
• Students are constantly reminded of one interpretation of fractions, and of ways to visualize the operations.
• The strategies are all built on ideas the students already understand: in this representation they apply the operations to whole numbers of grid squares.
• The representation provides an excellent context for generalization and for discussion of useful shortcuts.

In combination with other approaches, grid paper should help students become more comfortable with fractions.