Video: I didn't have to travel much this fall and winter. As a result, I had time to learn how to add videos to my website, something I had been reluctant to do in the past. Scroll down to MathEducation.page in this newsletter for links to new pages on the site, all of which include video components. Let me know if you find those helpful!
Better than video: see and hear me in person at one of my summer workshops. This year, I will present Hands-On Geometry as part of middle school math institutes on both coasts. Read all about it at the end of this newsletter!

Blog Posts
Here are links to posts on my Math Education Blog that you might find interesting.
If you are so moved, you may comment on the posts, and/or subscribe to the blog.
Towards Inquiry
In math class, clear explanations from the teacher are insufficient, as students often can't hear them. Pure exploration without teacher leadership and support doesn't work either. Teaching math is complicated: we need to combine strategies that seem mutually exclusive. This post is an annotated list of techniques for teachers who strive to navigate that contradiction. Choose one or two strategies to add to your repertoire!
Asilomar Report
Every December, I attend the California Math Council conference at Asilomar, a beautiful spot near Monterey. I usually both learn and teach there, sometimes in the same session. This year was no exception: I expanded my understanding of the geometry of conic sections; I co-presented "Lessons from Lew"; and I offered a session on Geoboards. As I do every year, I blogged about it: click here to see what I learned, and for many links.
Minimum Polyomino Cover
As you would know if you're familiar with my work, I'm a fan of geometric puzzles in the classroom. One reason is that they are interesting to both students and teachers. I recently become obsessed with a question I first asked in the 1980's: what is the smallest polyomino that can cover any n-omino for each n? I had my students explore this years ago for values of n up to 6. (See Polyomino Lessons, p. 17, and Geometry Labs, Lab 4.7). A few weeks ago, I came back to this problem and pretty much solved it for n=7. It was harder than I thought! I wrote about it here.
MathEducation.page
New on my Web site.
Fraction Arithmetic on Grid Paper
I drastically expanded this page. The basic idea is that when students think about fractions, they often need to think about two fractions which they are asked to compare, or add, or etc. Grid paper offers a dynamic environment where the student can be in charge, and choose a rectangle that is just right for the problem at hand. Read about this powerful and flexible paper-pencil tool here. (This includes many examples in five short videos and in written text.)
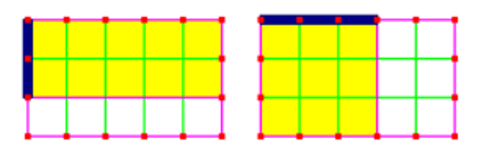
Which is greater, 2/3 or 3/5?
Off and On / Add Till It's Plaid
Many students have learned how to graph linear equations, but are not clear on what it means to say that a certain line is the graph of (for example) 2x−y=3. In a new lesson, I throw light on this is through looking at points which are not on the line: for a point (x,y), what is 2x−y equal to when the point is on or off the line? I then follow up with an exploration of what happens graphically when you combine two linear equations by addition, subtraction, and/or scaling. This leads to a strategy for solving systems. Both lessons involve interaction with graphs in GeoGebra, and explanatory videos. Check them out!
Number Pyramids
This is an activity for upper elementary or middle school students. First, students solve puzzles, like this one: in a number pyramid, each number is the sum of the two numbers below it; find the missing numbers.
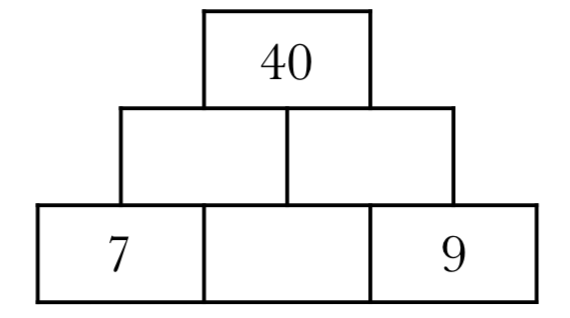
The puzzles get increasingly challenging, and eventually students are asked to create their own pyramid puzzles. Free download here.
