Completing the Square

Many secondary school teachers show students the derivation of the quadratic formula by completing the square, but they have little hope the students will follow or understand the argument. They do not worry too much about it, because as they see it, the main point is for students to learn the quadratic formula, and to know how to use it to solve quadratic equations. Understanding it is not a priority.

I disagree.

In fact, I believe the opposite: while I have no objection to students memorizing and being able to use the quadratic formula, this is much less important than it used to be. Nowadays, any quadratic equation can be solved by entering it in a CAS calculator or application, and pressing the Enter key. On the other hand, completing the square is a nice bit of algebra, with other uses for those students who will pursue more advanced work in mathematics. But even for students who will go no further than Algebra 2, it is interesting and accessible, and helps demystify the quadratic formula.

Well, it’s not accessible if taught to eighth or ninth graders strictly through the manipulation of algebraic symbols. I’ve done that, and to be honest, I was reaching perhaps 10% of my students. I was able to turn this around, and make the whole thing accessible to perhaps 90% of my students, by postponing this topic until Algebra 2 (10th / 11th grade), and by using a geometric approach based on the Lab Gear manipulatives.

Here is a summary of my strategy. The key is to break the long and complicated procedure into understandable chunks.

Using the Lab Gear, or some other algebra manipulatives, ask students to make a rectangle, then approximate a square using the same blocks (or tiles). In Algebra 1, this should be preceded by substantial work with the manipulatives. In Algebra 2, this can be done much more quickly.

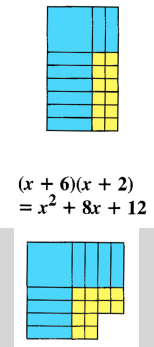
Doing this several times reveals visually what goes on, and makes it far easier to understand the process of completing the square.

These activities can be used to wrap up this phase:

- The Squaring a Binomial applet provides a way to discuss what students discovered with the blocks.

- The Completing the Square animation helps students put the process into words, and to generalize to non-whole-number values of b.

- This Geometry-Graphing Connection should yield much reflection and discussion, as it connects the Lab Gear images to the graphs of parabolas.

Having laid the foundation, you can now go full speed ahead.

Looking at increasingly complicated examples, you can make the point that if we have an equal squares equation, we can reduce it to two linear equations. For example, if `x^2 = 9`, then `x = 3` or `x = -3`. If `x^2 + 6x + 9 = 11`, then `x + 3 = sqrt(11)` or `x + 3 = – sqrt(11)`. (I avoid the phrase “take the square root of both sides”, which only encourages misunderstandings.)

After doing this a few times, it becomes possible to combine what was learned into an overall completing the square strategy to solve any quadratic equation by turning it into an equal squares equation. This in turn sets the stage for the algebraic derivation of the quadratic formula.

The whole approach is spelled out in Lesson 13.6 of Algebra: Themes, Tools, Concepts (free download), and in pp. 139-147 of Algebra Lab Gear: Algebra 1 (where to get it).