The Courses
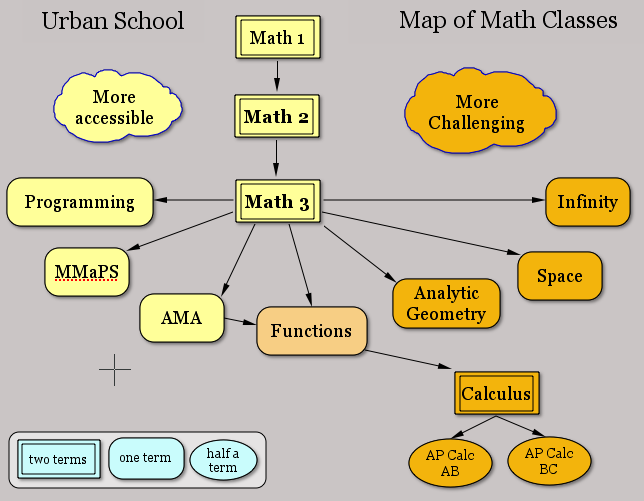
Here is a map of the courses we offer, followed by some commentary, and the course descriptions.
The Core
Our core classes are Math 1-2-3 and Functions. Our approach to teaching these courses is state-of-the-art and reflects the professional consensus as expressed for example by the National Council of Teachers of Mathematics Principles and Standards. In content, the courses are close to the traditional Algebra 1, Geometry, Algebra 2, Precalculus sequence, though some topics are tackled earlier or later.
Some features of the program:
We navigate between multiple representations of concepts, to reach different types of learners, and to provide more depth of understanding to all. This includes graphical, hands-on, technological, geometric, numerical, and symbolic approaches whenever possible.
Most instructional units are rooted in low-threshold, high-ceiling problems, which are interesting to both teachers and students. Everyone can understand the question, but getting to a full solution can be a real challenge.
Foundational concepts (such as equations, functions, and trigonometry) are investigated and practiced every year, at increasing levels of depth.
On a number of topics, our curriculum goes a lot deeper than tradition requires, and in fact many of our lessons serve as the backbone of a syllabus for the professional development of high school math teachers.
Most Urban students stick with math beyond the graduation requirement.
The Electives
We offer both standard and unusual electives. Like most high schools, we offer Calculus to our seniors, with the option to take the AB or BC Advanced Placement tests. The vast majority of students who have chosen to take the tests have done well, receiving 4s and 5s.
In addition to Calculus, we offer an exceptionally broad selection of electives, including accessible introductory courses in Applications, in Computer Science and in Statistics, plus three Honors classes. In Analytic Geometry, we teach traditional advanced high school topics (such as conic sections and vectors in three dimensions.) In Infinity and in Space we teach topics that are traditionally college-level topics, but with a high school-appropriate approach (polyhedra, infinite sets, group theory, chaos, fractals, and more.) Students who have taken both are unanimous in rating Infinity as more difficult than Calculus.
This extraordinary range of electives makes it possible for students to select courses that are appropriate to their interests, abilities, and priorities.
Course Descriptions
Urban School requires three years of math, taken in high school, for graduation. Students planning to apply to competitive colleges should take four years of math. Students considering a career in math, science, computers, or engineering should take four or more years of math, including Functions and challenging electives (Analytic Geometry, Calculus, Infinity, or Space.)
Math 1
In this course, students develop the concepts, skills and habits that form the foundation of high school mathematics. Many of the tools are algebraic, but almost all concepts are looked at in a variety of ways including geometric, numeric, and verbal approaches. Basic arithmetic and algebraic operations are modeled with physical manipulatives, making a geometric and visual connection with these operations. Our goal is for students to integrate and connect these methods.
Principal topics:
- Linear equations and graphs
- Introduction to the graphical representation of a variety of functions: continuous, discontinuous, step, linear, quadratic, exponential
- Equation solving by several methods: graphical intersection, numerical (systematic guess and check), "cover-up", algebraic symbol manipulation
- Number Sense: large and small numbers, scientific notation, estimation, opposites, reciprocals
- The distributive rule and factoring(1 credit)
Math 2
In this integrated course, students explore concepts through hands-on materials to create geometric conjectures, to use the language of algebra to describe some of these relationships, and to write formal proofs. Various algebraic concepts, such as simplification of square roots and variation functions, are approached geometrically. Slope and measurement are used to introduce trigonometric ratios. Writing computer programs and using dynamic geometry to create designs and figures, students deepen their understanding of geometric relationships as they experience the logic of computers.
Principal topics:
- Angles, polygons, parallel lines, circles
- Linear functions and systems of equations
- Distance and the Pythagorean Theorem
- Construction and proof
- Dynamic geometry with Cabri software
- Scaling, proportions, and variation functions
- Similarity and congruence
- Computer programming in Scratch: subprocedures and variables
- Sine, cosine, tangent in the right triangle and the unit circle
(1 credit)
Math 3
Math 3 continues and deepens our work with algebraic manipulation and graphical representation of functions as mathematical models. The practices developed in previous courses are expected to be in place so that the focus is on understanding concepts and demonstrating mastery. In particular, we expect fluency with algebraic symbols and notation. As the last course required for all students, Math 3 rounds out the basics of mathematical literacy, intensifies the challenge for students, and provides the foundation for upper level electives.
Principal topics:
- Quadratics
- Unit Circle Trigonometry, Law of Sines, Law of Cosines
- Exponents & Logarithms
- Arithmetic and geometric sequences and series
- Composition of functions and inverse functions
- Polar coordinates and vectors
- Complex numbers
(1 credit)
Advanced Mathematics Applications
Advanced Mathematics Applications is appropriate for students who need additional preparation in order to get ready for Functions. Key topics from Math 1-2-3 are reviewed. The course is also appropriate for any students interested in the history of mathematics and its applications to science.
- Topics in the history of mathematics may include: the development of our number system with influence from a variety of cultures, classical construction problems, geometric solving of equations, the development of algebraic reasoning and notation, equation theory, Fermat's Last Theorem, and approaches to area and volume.
- Topics in the Applications of Mathematics may include: quadratic and variation functions as they apply to Newton's Laws and motion; trigonometry as it applies to astronomy, geography, sound and light; rate of change applied to various systems; proportional thinking as it pertains to leverage, torque, optics, scaling and dimension; optimization problems applied to environmental science, economics and sustainability; logic and its applications to computer science and geometry.
(1/2 credit)
Prerequisite: Math 3
Programming
This is an introduction to programming concepts, using Alice, a new computer language in development at Carnegie-Mellon University, with the support of the National Science Foundation and Electronic Arts. Alice makes it possible for students to learn about algorithms and data handling, while developing individual creative projects involving the animation of 3D figures (video games, simulations, stories...)
Principal topics:
- Variables and scoping
- Passing parameters, returning values
- Subprocedures and modularity
- Looping and conditionals
- graphics/
(1/2 credit)
Prerequisite: Math 3
MMAPS
Mathematical Modeling and Probability-Statistics is an elective that concentrates on the applications of mathematics to the social and life sciences. This course is appropriate both for students who intend to go on to calculus as well as students who do not. Students apply concepts of counting, combinations and permutations to probability problems, and to the foundations of statistics. They use appropriate tools and techniques to interpret data, including especially computer software. The course also includes the mathematics underlying the sampling techniques used by scientists and pollsters.
Principal topics:
- Use of Fathom software to demonstrate and interpret data
- Analyzing the association of two variables from graphs
- Use of logarithms to straighten data
- Use of least squares line and correlation coefficient to find formulas for models
- Pascal's triangle and binomial distribution
- Simulations with dice and with software
- Sampling and sources of bias
(1/2 credit)
Prerequisite: Math 3
Functions
This course focuses on the topics needed for calculus. It is structured around functions as models of change, emphasizing that they can be grouped into families that model real-world phenomena. One goal of this course is to begin the transition toward more text-based college-level courses and more independent student learning. Students extend and deepen their knowledge and skills of the core curriculum (Math 1-3).
Principal topics:
- Functions: increased depth on composition, inverse and general fluency
- Functions: transformations, odd and even, limits, and end behavior
- Trigonometric functions, equations, and identities -- radians
- Exponential functions, e, and natural logarithms
- Polynomial and rational functions
(1/2 credit)
Prerequisite: Math 3
Analytic Geometry
This elective introduces complex topics at the pre-calculus level that are challenging and useful for advanced students, but not prerequisite for the standard calculus course. The daily problems can be more substantial than the standard work in the core curriculum. There is a focus on moving fluently back and forth from a variety of algebraic forms to graphing in different coordinate systems in two and three dimensions. Students derive equations from definitions and general principles.
Principal topics:
- Vectors in three dimensions
- Conic sections
- Polar coordinate equations and graphs
- Parametric equations and graphs
- Binomial Theorem
- Infinite Series and complex numbers (Euler's formulas)
(1/2 credit)
Prerequisite: Math 3
Space
This advanced geometry course includes a thorough exploration of symmetry, including an introduction to group theory, and extends students' geometric experiences into three and four dimensions. Many hands-on 3D building labs, creative projects, and the reading of mathematical fiction illustrate the concepts.
Principal topics:
- Geometric transformations
- Symmetry groups, tessellation, Escher – art projects
- Matrices
- Three-dimensional geometry, especially polyhedra
- Flatland and the fourth dimension
- Zome System construction kit
- Computer labs, using Cabri and Cabri 3D software
(1/2 credit)
Prerequisite : Math 3
Infinity
In this course, students discuss ancient paradoxes about infinity, and learn how Georg Cantor resolved them. This discussion launches our most theoretical course. Infinity includes a strong emphasis on formal proof and an introduction to chaos theory and fractal geometry, two computer-centered branches of mathematics. Connections are made with literature and philosophy.
Principal topics:
- Introduction to set theory and infinite sets
- Different-sized infinities, transfinite numbers
- Proof by contradiction, proof by induction
- Iteration and recursion
- Fibonacci numbers
- Dynamical systems and the Mandelbrot set
(1/2 credit)
Prerequisite: Math 3
Calculus
The goal of this course is to provide students with a solid foundation for subsequent college level courses in mathematics and other disciplines. The course is focused on differentiation, integration, and their relationship. The math concepts are enhanced by applications relating to geometry, physics, economics, ecology, and medicine. Students are expected to take full responsibility for their learning by using the text and applying all the skills and content learned in previous courses. They are expected to navigate between graphical, numeric, analytical and verbal representations of problems and to use the graphing calculator appropriately.
Principal topics:
- Differentiation
- Limits
- Integration
- Graphical analysis
- Introduction to differential equations and slope fields
(1 credit)
Prerequisite: Functions
AP Calculus AB
This half-trimester course provides intensive preparation for students who wish to take the AB Calculus Advanced Placement exam. It is a follow-up to the calculus course, and helps students solidify their understanding, while they develop test-taking skills.
(1/4 credit)
Prerequisite: Calculus
AP Calculus BC
This half-trimester course provides intensive preparation for students who wish to take the BC Calculus Advanced Placement exam. Since the BC curriculum includes a number of extra topics beyond the Calculus course, the course strikes a balance between review and the introduction of new ideas, primarily Taylor series.
(1/4 credit)
Prerequisite: Calculus