Sums Of Consecutive Numbers
9 can be written as a sum of consecutive numbers in two ways: 2 + 3 + 4 and 4 + 5.
For each number from 2 to 34, find all the ways to write it as a sum of consecutive natural numbers.
As you work on this problem, think about the following questions:
- What numbers are the sum of two consecutive numbers?
- What numbers are the sum of three consecutive numbers?
- What numbers cannot be written as the sum of consecutive numbers at all?
- What is a good shortcut for adding strings of consecutive numbers?
- What is the average (mean) of a string of consecutive numbers?
- How is the average related to the sum?
In general, how can you predict the number of ways a number can be written as a sum of consecutive numbers?
A slightly different version of this, with Teacher Notes, is here. (Click on Staircases.)
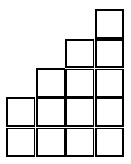
Building Block Numbers
Food for Thought
Sally tried to order 13 chicken "nuggets" at the fast food store. The employee informed her that she could only order 6, 9, or 20. Sally realized she had to decide between ordering 6 + 6 = 12, or 6 + 9 = 15.
- What numbers of nuggets can be ordered by combining 6, 9, and 20?
- What numbers cannot be ordered?
- What is the greatest number that cannot be ordered?

Two Building Blocks
In the previous problem, 6, 9, and 20 were our building block numbers. It is interesting that all numbers beyond a certain number can be ordered. To think about this further, let us look at some more examples, using only two building block numbers.
- You have an unlimited supply of dimes(10 cents) and quarters(25 cents). What amounts can be obtained, and what amounts cannot be obtained by combining them?
- At Fred's Kitchen Supply, cabinets are available in two lengths: 3 feet and 5 feet. By putting cabinets end to end, walls of different lengths can be accommodated. Imagining that kitchens can be arbitrarily large, what length walls are possible to line exactly with cabinets? What lengths are impossible?
- What numbers can be obtained by adding the numbers 6 and 9 as many times as you want? What numbers cannot be obtained?
- In 1958, it cost 4 cents to mail a letter in the United States. In 1963, it cost 5 cents. Imagine you have an unlimited supply of 4 and 5 cent stamps. What amounts can you make? What is the largest amount you cannot make?
Generalize: By now, you are probably aware that some pairs of building block numbers work better than others.
- Which types of pairs allow us to build every number beyond a certain point?
- For the other pairs, what do they allow us to build?
A Visual Strategy
It would be interesting to know how to find the greatest impossible number for a given pair of building block numbers, if it exists. We will investigate the problem using 5 and 7.
| 0 | 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | ... |
| ... | ... | ... | ... | ... |
Write the numbers from 0 to 39 in an array like this:
Then, circle all the numbers we can get by adding 5's and 7's. Follow the following process:
- Circle the multiples of 5, since we can get them. (Remember that 0 is a multiple of 5.)
- Circle the numbers that are equal to 7 plus a multiple of 5.
- Circle the numbers that are equal to 14 plus a multiple of 5.
- Continue in this fashion, using 21, 28, etc as your starting point, until you have circled enough numbers to know what numbers can and cannot be built from 5 and 7.
Think about the strategy we followed: first we organized the numbers in five columns (why five?), then we circled the numbers we can get in an organized fashion. Would you know how to apply this method if the building blocks were
- 5 and 6?
- 4 and 6?
- a and b?
What went wrong in the case of 4 and 6?
If you can follow the procedure in the case of building blocks a and b, you might be able to find a formula for the greatest impossible number in terms of a and b, if it exists. (The answer can be found in my letter to the NCTM journal.)
Square Pairs
Arrange the whole numbers from 1 to 18 into nine pairs, so that the sum of the numbers in each pair is a perfect square.
For what numbers other than 18 is this possible?
It turns out that after a certain point, it is possible for all even numbers.
With Gord Hamilton and Kiran Kedlaya, I co-authored a paper on this problem for The College Mathematics Journal published by the Mathematical Association of America (September 2015): Square-Sum Pair Partitions. The paper earned us the 2016 MAA George Pólya Award.