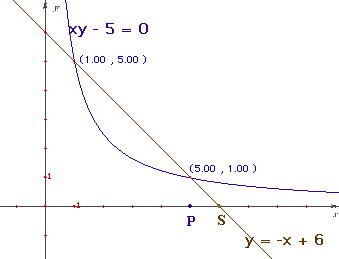This is a mega-unit, spanning content from middle school, all the way to what one might call "teachers' mathematics." Look through it, and see which parts you can use.
It is largely based on material from Algebra: Themes, Tools, Concepts (free download: ATTC). You can find some teacher notes and solutions in the ATTC Teachers' Edition.
- Part 1: `x+y=S`, `xy=P`
- These are the foundational lessons of the unit: they lay the foundation for everything else. The first two both start with reasonably realistic "real world" contexts.
- Constant Sums One possible side use of this lesson is to derive and justify the rules of signed number addition, which presumably should extend the line into quadrants 2 and 4 — and in the case of a negative sum, quadrant 3. (Note for math book nerds: the lesson is in part an homage to a textbook author who specialized in fun real-world connections. Can you recognize him?)
- Constant Products One argument for including the constant product graph in middle school is to help kids know early on that not all graphs are lines, and moreover that not all curves are parabolas.
- Analyzing Graphs A connection is made to factoring trinomials — a key idea of the whole unit, which was suggested by my co-author Anita Wah. My first reaction was that this was too abstract, and at first it sure felt that way. However as we got more comfortable with it, it turned out to make for great discussions in our Math 1 classes.
- Edited version of the above three lessons
- Five Representations We ended up making this writing assignment a regular end-of-year feature of Math 1. It connects the ideas from this unit with the Lab Gear representation of trinomial factoring, and makes for a great review activity. It helps students consolidate and elevate their understanding, and for some students, it offers one more chance to grasp some of these ideas if they didn't fully master them the first time around. Each student is supposed to choose their own trinomial, and one way they can create the graphics is by using some of the links on the "Five Representations" page.
- GeoGebra Applet (and file) by Henri Picciotto. It complements the worksheets, and can help structure some discussion of "Analyzing Graphs" as well as preview some ideas that are useful in Parts 3 and 4 below.
- Cabri figures: 1 and 2 by Henri Picciotto
- Cabri figure by Ari Klein
- Part 2: `ax+by=c`
- Standard Form for linear functions. As it turns out, constant sums provide a great jumping off point to introduce the standard form for the equation of arbitrary lines.
- Part 3: Geometric Connections / Optimization
- Rectangles with constant perimeter are related to constant sum relationships. The first two lessons pursue this topic with some area maximization problems. Rectangles with constant area are related to constant product relationships. This section's final lesson explores a perimeter-minimizing problem.
- Constant Perimeter
- Advanced Penmanship
- Edited version of the above two lessons
- Constant Area
- A hands-on lab, and a completely different geometric connection (similar triangles):
- Perspective
- Part 4: Quadratic Connections
- Find the Dimensions. This can work as a way to tie many ideas together for algebra students (probably Algebra 2), or as an introduction to the next item.
- A New Path to the Quadratic Formula, by Henri Picciotto. This came to me some years ago when grading the "Five Representations" assignment. It applies that kind of thinking to proving the quadratic formula, with no recourse to either completing the square or parabolas. You can work through the ideas yourself using the worksheet as a guide, or read the article (shared on my site with permission from The Mathematics Teacher), or follow the argument step by step on the video, or using the slides, or some combination thereof. (The GeoGebra file is what I used to make the video and the slides.) I have done this lesson many times with teachers, and a few times in precalculus classes.
- Worksheet | Article | Video | Slides (Online, Keynote) | GeoGebra