If you are planning to do the first lab, you should do it first. Other than that, the labs do not have to be done in order. If you don't have a lot of time for this, in a high school geometry class, do the first and last lab, or just the last one. In middle school, do the first and second lab, or just the second one.
1. Discovering the SuperTangrams
Print and duplicate "Polytans" (Geometry Labs 4.1).
#2 is challenging, and you should encourage group collaboration to help those students who are getting stuck. You need to decide whether to tell the class how many distinct superTangrams there are (fourteen).
After #2 has been answered, you should distribute superTangram sets, which will make it easier to work on the remaining problems. To avoid mixing up the sets, do not give the same color to neighbors. Tell them that there are fourteen pieces per set, and warn that at the end of class, fourteen pieces should find their way back into the bag.
2. SuperTangram Polygons
Print and duplicate "SuperTangram Polygons".
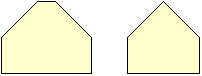
This lab offers a fun opportunity to become familiar with the standard names of various polygons: triangles, squares, rectangles, parallelograms, right trapezoids, isosceles trapezoids, pentagons, hexagons, octagons. As students discover them, the names of the figures can be added to the table, beneath the ones that are already listed. Further distinctions can be added by paying attention to symmetry within given categories. Two superTangram shapes are common enough to deserve a special name: the hex-house and the pent-house, illustrated below. (They are symmetric hexagons and pentagons with two consecutive right angles.)
3. Selected SuperTangram Puzzles
These are "just for fun" puzzles. They are reminiscent of the puzzles that can be investigated with tangrams and pentominoes, but they are generally more difficult than either one.
Print and duplicate "Selected SuperTangram Puzzles".
#1 consists of easy, warm-up puzzles. #2-5 increase in difficulty with the number of pieces used.
If your students are not familiar with the meaning of "convex", a simple definition in this context is: a convex polygon is one whose angles are all less than 180 degrees. Discuss this definition with a few examples before students attempt #5.
Fourteen-piece puzzles: if one is using all the pieces, only four solutions are known to #4. Two of them are convex, and make nice, tough puzzles. (Print and duplicate SuperTangram Hexagons. These puzzles can also be found in the Supertangram Puzzles book, along with six more 14-piece convex figures (not symmetric). The latter were found by Miroslav Vicher via computer search. The search also revealed that the symmetric 14-piece hexagons I found by hand can be solved in 747 and 236 ways respectively.
Andris Cibulis found a four-layer convex figure:
Many more puzzles with a wide range of difficulty are in the Supertangram books. (Free downloads.)
4. Scaling SuperTangrams
Print and duplicate Scaling SuperTangrams.
For this lab to be most effective, it should follow Lab 10.3: Polyomino Blowups in Geometry Labs, (or some other introduction to the concept of the relationship between scaling factor and ratio of areas,) and/or the Pentomino Blowups lab on this site.
This is the richest lab of the set. It combines puzzles that range from easy to challenging with some interesting mathematics about similar figures and the square root of two. Note that only five other supertangrams can be scaled to all four different sizes. (In the notation I shared here, this lab is about B. The other pieces that work are H, T, h, s, and t.)