- Article outline:
- Introduction
- Multiple Representations
- Teacher Eclecticism
- Math Education Research
- Fads
- A Possible Framework?
Introduction
When I say "there is no one way", I am referring to multiple representations of concepts, and also to the intimately related idea of multiple pedagogical approaches. This does not mean I believe all “ways" are legitimate at all times or all ways are equally valid in any situation. Still, I insist that it is a mistake to put all of one’s eggs in any one instructional basket. One’s growth as a teacher is largely about learning many ways to teach important concepts, so as to reach more students, and to deepen all students’ understanding. How many ways you can think of something is an excellent measure of how well you understand it.
But doesn’t using multiple approaches confuse the students? Well, yes, it may. It is especially confusing when connections are not made between the approaches, or when the teacher’s understanding of an approach is superficial. But we run greater risks if using a single approach. Multiple representations (and thus multiple approaches) are dictated by the math itself. This is what I want to discuss first, using examples.
Multiple Representations
Whole Numbers
A good way to think about whole number subtraction is with the help of counters. If I start with ten counters, and remove three, how many are left? Another good way is to think of whole numbers as sitting on a number line. If I start on the 3 and count up to the 10, how many steps did I take? Or, I can use Cuisenaire rods: what is the difference between the orange rod and the light green rod?
For place value, I can use counters again, possibly using the “exploding dots” version, or an abacus. Or I can use base ten blocks, which help the students see successive powers of ten geometrically. Or I can have students make their own base ten materials using beans and tongue depressors.
For multiplication, I can use counters again: 3 times 5 can be represented as 3 sets of 5 counters. Or, I can arrange the counters in a rectangular array, which allows me to see that 3 times 5 equals 5 times 3, which is not as obvious in other representations. (Also, it previews the area model for multiplication, which helps with algebra and even calculus.) Or I can do 3 hops of length 5 on a number line. Or I can learn to count by 5’s— a condensed version of the number line model.
The power of math is precisely that the same structure (in this case whole number arithmetic) describes many different phenomena. Understanding these representations, and their relationships with each other is a lot more powerful than teaching this subject in a single way. It respects students’ intelligence, and it is more true to the math: numbers are indeed all those things, irrespective of your pedagogical orientation. If a teacher is comfortable with all the models, uses them strategically, and helps students think about the connections, multiple representations are illuminating, because they reveal the many meanings of the underlying math.
Fractions
The same is true about fractions: the widely used “pie” representation provides a great connection to angles and to time as seen on a clock. A number line representation emphasizes that a fraction is a number, and reveals its relative size. The "well-chosen rectangle" representation on grid paper facilitates computation and helps to introduce the idea of common denominator. As far as I know, this last representation is underused. And yet it is an accessible model that can be the foundation of important discussions, and can be used for many different fractions topic. Of course, it should complement (not replace) other approaches.
Here is an example: which is greater, `2/3` or `4/7`?
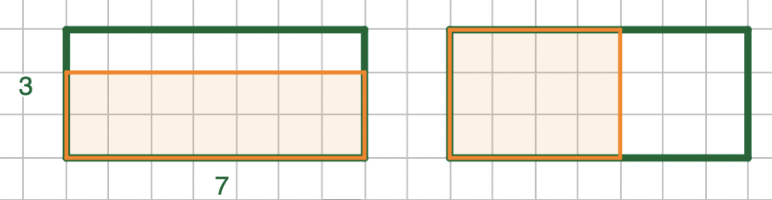
Using 3 by 7 rectangles (as suggested by the denominators) makes it easy to see both fractions as parts of the same unit. Counting reveals that `2/3` is 14 squares, or `14/21`, while `4/7` is 12 squares, or `12/21`. Which is greater has been made clear. Those very same rectangles can help us think about `2/3 + 3/5` or `2/3 - 3/5`. See a full introduction to this representation (including homemade videos) here.
Algebra
Or take the use of letters in algebra. Sometimes, `x` is an unknown, and to find its value we learn to manipulate symbols. Sometimes we use it to make a general statement about algebraic expressions, for example this identity `2x = x + x`. (Algebra manipulatives can help with that.) Sometimes it’s a variable, and we explore what happens to an expression as `x` varies. Tables, graphs, and function diagrams can help us understand that. Sometimes `a`, `b`, and `c` are parameters. They constrain an expression, but they are not unknowns or variables.
A well-intentioned but pedagogically clueless mathematician once commented that variables are easy to teach: just patiently explain to students that they behave just like numbers!
In fact, the reality is that it is a good idea to use many representations: tables of values, graphs, manipulatives, symbol manipulation, and function diagrams. Done well, this is not confusing: it’s illuminating. The historically catastrophic failure rate in the traditional Algebra 1 course is largely caused by the naive belief that patient explanations of how to move `x`’s and `y`’s on a piece of paper is the only way to go, as long as you follow it by mind-numbing and meaning-free practice.
Trigonometry
Or take trigonometry: the sine can be seen in a right triangle, or in a general triangle, or in the unit circle, or in a Cartesian graph. This is not because a teacher decided that. It’s in the math itself — and it gives us multiple approaches to the concept, with opportunities to make connections between them. (Here’s one such connection.)
Multiple representations reveal the many-fold meanings of math concepts. To make that less confusing, the answer is not to limit students to a single representation, even if you’re proud of how good you are at that particular one. Instead, give some thought to a proper sequencing of the representations, encourage students to use the representations that makes sense to them, and especially be sure to connect the representations to each other.
Teacher Eclecticism
And it's not just multiple representations! "There is no one way" also applies to pedagogy. A few years ago, Dan Meyer attended my Making Sense in Algebra 2 workshop had an interesting criticism. He pointed out that I presented no coherent pedagogical framework for the activities I shared. Good point! I did not present a coherent framework because, well, I did not have one to present.
Certainly, the title of the workshop captured my goal: the activities I shared were intended to help students make sense of Algebra 2 content. But that is not a pedagogical framework. In fact, I think every activity was different: I used labs, spreadsheets, kinesthetic strategies, measurement, graphing technology, games, slides/lecture (yes!), big anchor problems, and perhaps other formats.
According to Merriam-Webster:
Eclectic: selecting what appears to be best in various doctrines, methods, or styles
That pretty much describes my stance as an educator.
During my four-plus decades in the classroom, I've seen many math edu-fads come and go: new math, individualization, manipulatives, problem-solving, group work, constructivism, constructionism (yes, that's a thing), portfolios, complex instruction, differentiation, interdisciplinary-ism, backward design, coding, rubrics, problem-based instruction, technology, Khan Academy, standards-based grading, making, three acts, flipping, inquiry learning, notice-wonder, growth mindset... not to mention various generations of standards.
It doesn't take long for a conversation between teachers to include something sarcastic about the fad du jour. By being sarcastic, we put up an umbrella to try protect our sanity from the ideas raining on us from administrators, academics, and yes, even colleagues. I will go further, and boldly say to the proponents of the current pedagogical panacea: I'm sorry, but whatever "evidence-based" product you're selling today, I'm not buying. The research it is based on is flawed. The anecdotes that support it only apply to specific circumstances which are not easy to replicate. In short, nothing works.
I guess that sounds cynical.
But I am the opposite of cynical! Nothing works for every student, every class, every period, every day, every teacher, every department, every school, every district... That is just a fact. There is no one way. But this is what makes our job interesting! We need to be eclectic, and select "what appears to be best in various doctrines, methods, or styles." Instead of rejecting the fads wholesale, we need to consider each one as it comes along, as all (or almost all) have some validity. Instead of shutting our classroom door and continuing business as usual, we should keep it wide open. Without becoming a dogmatic across-the-board adopter of each pedagogical scheme, we need to learn what we can from it, and incorporate that bit into our repertoire. This is how we get the sort of flexibility that makes for good teaching. If we do that, our lessons will not fit a standard mold. Quite the opposite: they will depend on the myriad variables that make teaching such a complex endeavor.
Thus, when I share the materials on this website, I am not saying they are sure to work for you just as they are. Au contraire! Take from it what you want, and adapt it to your own classes, your own personality, your own math background, your own school schedule, you own beliefs. And let me know how it goes!
When I articulated this eclectic stance in a blog post, the response from teachers was mostly enthusiastic and supportive, but there were reservations from some. Here are four points that were raised in response:
- Not all math education research is flawed.
- One should oppose faddism, not coexist with it.
- Asking for the big ideas underlying good lessons is legitimate.
- And in any case, it is not true that I don't have a coherent pedagogical framework.
I'll address these in order.
Math Education Research
Aran Glancy says: "characterizing all educational research as flawed is unfair." Of course, he is right. The point I was trying to make was that even valid research that is used to support the unrealistic claims at the core of various fads should not be generalized beyond reason. As Aran puts it: "the issue is much, much less about the quality of the research and much more about how it is misused to create the fad". Fair enough. We agree on that.
- As evidence that I don't think all research is flawed, here are links to blog posts in which I praise specific bits of ed research:
- Complex Instruction
- Random Groups
- The Thinking Classroom
- and a guest post which cites many studies:
- Grades: What Does the Research Say?
So far, so good. But Aran took exception to my statement "I like research that confirms my beliefs, and appreciate the work that goes into it." I am not retreating from that. Much research claims to prove things I know are false, or at any rate not useful to me. I have neither the time nor inclination to analyze those papers.
For example, I was told that short periods are better than long periods for teaching math, because someone found a correlation between higher test scores and shorter periods. (If I remember right, this argument was used by administrators at a school that had a very strong math program, which was catastrophically undermined when moving to short periods.) While I am sure some good teaching can happen in shorter periods, I believe it's absurd to make a blanket claim that those are superior to longer periods. (See Math in the Long Period and Teaching in the Long Period for an explanation of my views on this.) If there is such a correlation, it could be due to the fact that it is schools that were less successful on tests that felt a need to try block schedules. Or it could be that the tests measured something other than depth of understanding. Or it could be something else. I don't have time to look into it. I hope and assume that someone else's research sooner or later will establish the opposite result.
Here's another example. I'm a big fan of the "growth mindset" fad, and in fact have been making some of those points for years. Having some research to back this up is excellent. But frankly, some of the research is hard for me to take seriously. The claim that being exposed to this concept in a slide show is sufficient to change a student's mindset is hard to believe, even if some short-term effects can be observed. What may have a lasting effect on student mindset is restructuring one's teaching to make clear in practice, not just in words, that students can get better at math. This would include such policies as extending exposure, lagging homework, de-emphasizing grades, valuing test corrections, making explicit every day that getting it wrong is often a necessary stage on the way to getting it right, and so on. In other words, a classroom culture that challenges the dominant culture. I would love to be able to point to research that supports those things, so if someone reading this post can do a study comparing such practices with the single slide show approach, I'd love to know how it turns out.
The fact is that research is influenced and framed by the researcher's values. As teachers, we don't have time, and most of us don't have the interest, to survey the literature, evaluate papers, and impartially reach conclusions. We need to find math ed researchers who share our values, and use their results to refine our practice, and to dialogue with administrators. For example, if equity is an important goal for you, find the researchers who share that concern. Their work is likely to be useful. If you prioritize understanding over memorization, or collaboration over competition, find the research that is about that. And so on. But to be honest, it will often be more fruitful and practical to get your ideas from fellow teachers.
Some years ago, at a conference, I saw a math ed prof who was an expert on the learning of geometry. I had recently read one of his papers, and I said to him: "Your research confirms my beliefs!" Without a moment's hesitation, he replied, with a big smile: "That's what it's for!" Was he joking? I don't think so. That is indeed what it is for.
Fads
Patrick Honner wrote: "Oddly, this seems a bit like a defense of edu-faddism. We can always learn something from fads, so keep them coming!" I certainly didn't intend to say that, but it is true that I have learned something from almost every one of the fads I listed above, and probably from some I did not list. So yes, I have learned to coexist with the fads. None of them have all the truth, but most have some piece of it, and I'm open to that. Like I said, I'm eclectic, and I reject the defensive and cynical stance that rejects any and all new ideas. Keep'em coming! I trust myself and my colleagues to separate the useful from the ridiculous.
The reality is that fads will always be with us. Consider their life cycle: researchers uncover an important idea about how children learn. They care about this, and find ways to spread the word about their discovery. Sometimes their discoveries are the result of questionable studies, but even if the results are valid, they can be misinterpreted or overgeneralized. In any case, they gain further traction as administrators want to spread them into their schools and districts, usually with the best intentions. Some consultants tap into this phenomenon, and become the carriers of that gospel, until the next fad comes along. I see no way of stopping this. Many people want to help teachers, without being teachers themselves, so they contribute to one or another link in that chain. I appreciate their efforts, even if I don't buy their often naive claims.
In addition to these grand fads, we also have teacher-initiated memes, which I unfortunately lumped together with the fads in my post. Those are often more useful and less pretentious, as long as we avoid the temptation to see them as more than what they are. One example is Dan Meyer's "three-act" math tasks.
Speaking of Dan Meyer — he followed up: "Loved the workshop. I wasn't asking for more fads, though. The opposite. The Internet is awash in interesting math lessons. I'm interested in the bigger ideas about learning that undergird them, that survive fads, that generate more lessons." I too am interested in such ideas, but I stand by my call for eclecticism. Teachers have little time for theory and are happy to collect interesting lessons from the Internet, from conferences, or from colleagues. I am happy to contribute such lessons. I have been prolific, and my curriculum creations over the decades have varied widely. Trying to stay within a framework would have probably paralyzed me.
By staying in the classroom for 42 years, and by teaching just about everything from counting to calculus, I have come across widely different teaching challenges, which have led to widely different pedagogical responses. This is true of all teachers: we don't have the luxury of constraining ourselves to a single theory, because our work does not allow it. We get ideas from many sources, and evaluate them by using them. The best of those ideas end up in our repertoire. We have no choice but to be eclectic.
A Possible Framework?
That said, Dan's search for big ideas that can support teaching and learning is of course completely legitimate. Moreover, a colleague who is very familiar with my work tells me that whether I know it or not, I do in fact work within a pedagogical framework. In thinking about her comment, I remembered that at some point in the 1990's, when Anita Wah and I co-authored the textbook Algebra: Themes, Tools, Concepts, we did develop a bit of a pedagogical framework, one perhaps broad enough and flexible enough to accommodate an eclectic teacher. Here is a visual representation of it, a map of sorts:
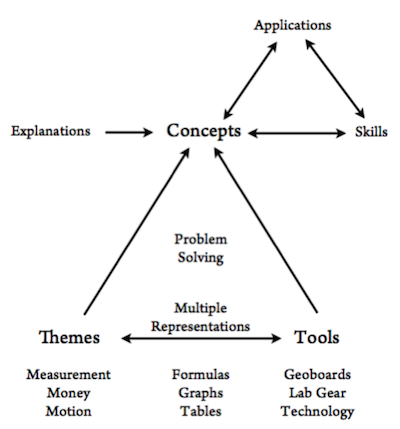
Traditional pedagogy stays at the top, as it is based on the belief that skills practice and teacher explanations are sufficient to build student understanding. Understanding acquired this way, plus practice, allow the student to apply the ideas.
Would that it were that simple.
In my experience, concepts are best developed by spending a lot of time at the bottom of the map. The interaction of themes, representations, and tools provides a foundation on which concepts can develop. (In the map, I mention examples of themes, representations, and tools. Of course, those lists are not meant to be exhaustive.)
The idea is not to rule out explanations and practice, but to give them a chance of being effective.
This is pretty complicated, you say? Well, yes, it is.
Where does one start? In thinking about curriculum one often starts with a concept one wants to teach. From there, one can look at the bottom of the map for ways to build up the necessary experiences for students.
But it's also possible to start with a theme. I developed a whole lot of curricular material based on an exploration of how the theme of area interacts with various tools and representations, and leads to various concepts. In fact, I wrote an article about it, where I included this out-of-control figure.
Or one could start with a tool, and ponder what uses it may be put to. I have done a lot of that, as you can see throughout this website: the Lab Gear, the geoboard, Zometool, pattern blocks, function diagrams, graphing technology, the interactive whiteboard, etc... (See the links in For a Tool-Rich Pedagogy.)
Shira Helft introduced me to the concept of the knife: a learning tool that is powerful and versatile, like a kitchen knife — as opposed to specialized tools such as peelers, corers, slicers, pizza cutters, and so on. She is right: teachers should prioritize multi-use learning tools, especially at the start of their career. Later, they can diversify, as I did.
The wielding of learning tools, the exploration of interesting contexts, and the use of multiple representations add up to a fertile foundation for learning math. They make it possible to center problem solving and teacher-guided discovery. Perhaps you feel this is a hodgepodge, not a framework? Fair enough. What can I say, there is no one way!

