Big-Picture Planning

This article is about the planning that precedes and constrains lesson planning in math education, mostly in middle and high school. I make suggestions on how to plan a departmental program, a course, and the units within a course. This big-picture planning is best done during the summer, in collaboration with colleagues.

Organizing things in a strictly logical sequence is almost always a mistake: such sequencing may make sense to a mathematically sophisticated person, but it is not necessarily best from a pedagogical standpoint. Doing things in a certain order because tradition requires it is another loser, as traditional sequencing is often without any basis in how children actually learn. Finally, looking at lists of standards is useful when checking for completeness or compliance, but it is not particularly helpful in developing a plan.

Effective sequencing, like everything else in teaching, requires paying attention to what happens with actual students. I did this for 42 years, and came up with some ideas you may find useful. In Nothing Works, I shared an overview of some key ideas, which I expand in this article.

I realize that many teachers have no control over the big-picture plan for the classes they teach. Still, I hope this article can help in conversations with colleagues and administrators.

In my article on the Common Core I discussed in detail a realistic sequencing of topics across the four years of high school, with close attention to the standards as they appear in the recommended "pathways". I will not duplicate that here, but I will mention two big ideas about sequencing across the grades.

Is the topic age-appropriate? Mysteriously, not much attention is paid to this. For example, tradition requires completing the square and the quadratic formula as topics for Algebra 1, In my experience, it is much easier to teach this in Algebra 2, to students who have a little more mathematical maturity. This in turn frees up precious time in Algebra 1 to reinforce the sort of basics that we find so frustrating when they are missing later on.

Can the topic be covered in a single course? Some topics are important, but difficult for some students. Some are important, and wide-ranging. It's a good idea to spread such important topics out over more than one unit, and sometimes more than one course. One example of that is linear, quadratic, and exponential functions, which can be approached in different ways at different levels, from Pre-Algebra to Precalculus. Another example is trigonometry, which can be distributed among Geometry, Algebra 2, and Precalculus.

If you want to teach for understanding and retention, you need to approach important topics repeatedly, and from different points of view. This includes different representations of concepts, and different learning tools to get at them. One reason for this is that since students have different backgrounds, experiences, and talents, some approaches will work better for some students, and other approaches will work better for others. Another reason is that extended exposure helps make ideas stick in a way that rushing through them cannot. Finally, making connections between multiple points of view is an important part of understanding.

But multiple approaches take time, and whether you like it or not, the only way to make time is to take out or reduce unnecessary parts of your program. This needs to happen first. (Even if you do not have the option of taking topics out, you might still be able to change the amounts of time allotted to various items.)

Almost certainly, many things can go. Any topic that is only there because it's a personal favorite should at least be considered for deletion. Any topic that is unconnected to things that come before or after can probably be skipped. Any topic that is only there out of habit should be eliminated. Any topic that only reaches a handful of students should be taken out as it is wasted time for the others. (Do those super-hard topics in the math club, or move them up the grades to a level where more students have a chance of understanding them.)

Most controversially, you should consider spending less time on techniques and procedures that have been rendered obsolete by the availability of technology:

- Less time on paper-pencil multi-digit multiplication and division

- Less time on complicated factoring problems and techniques

- Less time on complicated equation-solving

- Less time on complicated manipulation of radicals

All of these things can be done faster and more accurately by machines. Speed and accuracy in computation are no longer legitimate priorities for math education — if they ever were.

The reality is that for most learners many of the more complicated techniques, and the hours of practice needed to master them, do not shed any light on the underlying concepts. Quite the opposite: in some cases, they have been designed precisely to get accurate results without having to think or understand.

You may feel I am reckless in making these suggestions. I am not. I want you to be careful because the concepts behind all these manipulations remain essential.

- Multiplication and division will of course always be important, and there are many interesting things you can do to help students make sense of them, for example exploring arrays with Base Ten blocks, estimation, and mental arithmetic.

- The concept of factoring polynomials will always be important, and a student who cannot factor anything does not understand the distributive law. That is pretty much catastrophic from the point of view of developing any sort of symbol sense. The area model can help, perhaps using Lab Gear or some other algebra manipulatives.

- Building connections between equation-solving, graphs, and tables is a good way to develop sense-making. Also: solving simple equations mentally is for some reason not a standard activity. It should be!

- An interesting way to talk about radicals is geometric (as developed in Geometry Labs, 8.4-9.4). Simple manipulations of radicals remains important for communication and reasoning. For example, it is useful to understand that `1/sqrt 2 = sqrt 2 / 2`, if only to confirm two answers to a geometry problem are equivalent.

In any case, I am confident that you will reach more students with deeper understanding of these important concepts if you prune your curriculum. One step at a time, and in consultation with your colleagues, cut back on side topics and complicated manipulations and replace them with intellectually engaging work. One benefit of this approach is that it is more interesting to more students — a necessary ingredient for learning.

After settling the big picture of where each topic belongs, and after pruning the content at each level, you still need to sort out the sequencing within the school year.

First decide what the main topics would be. The main topics, not all the topics you can think of. Even if you're forced to work with an overstuffed list of standards, the first step is to prioritize.

Organize the main topics into units, maybe six to eight units per semester. In general, something that doesn't deserve a unit or fit in one probably shouldn't make it into the program. Also save a stretch at the end for review, or just as cushion if things take longer than expected.

When in the school year? Difficult and important topics should not be introduced in May! By then both students and teachers are tired, and there is little chance of success. Teach those topics as early as possible. There may also be some traditionally late topics that can be useful early on. For example, a study of inscribed angles is late in many textbooks. Yet an exploration of this topic has only very few prerequisites, and it can be used to practice angle basics in an interesting context. (I did this very early in my Geometry class, and shared that approach in Chapter 1 of Geometry Labs.)

Spiraling. Repeated and extended exposure to the most important topics should be a key ingredient in your plan. However spiraling can be overdone, and result in an atomized curriculum consisting of chunks that are so small that students don't get enough depth on each topic. Also, in some spiraled curricula the topics addressed by each problem or each lesson are not always explicit. This makes such programs more difficult to use. On the other hand, it takes too much work to work out a spiral approach to a traditional, not-spiraled textbook. As a department chair, I needed a structure that would be simpler and more transparent, as my colleagues quite rightly wanted to know what was going on. In Reaching the Full Range, I suggest easy-to-implement policies which provide the advantages of both spiraling and depth.

Review? It is widely believed that one should start the year, and then each unit and even each lesson with review of relevant past material. Of course, I understand why that is a standard practice, but I believe it is counterproductive. Over time, it tells students "you don't need to remember anything — I'll make sure to remind you." It is also profoundly boring for the students who don't need the review, and takes away from the excitement of starting something new. It is especially catastrophic to start Algebra 1 with a review of arithmetic. The students who need it won't get it, and those who don't will be disappointed.

Separating related units.This is not to say that review is not important! Quite the opposite. All I'm saying is that it's the wrong way to start a course or a unit. It is far better to review by using homework, subsequent class work, the "full range" strategies mentioned above, and if need be out-of-class support structures. Another good strategy is to separate related units. Doing so provides one way to support spiraling and necessary review. (This is spelled out here.)

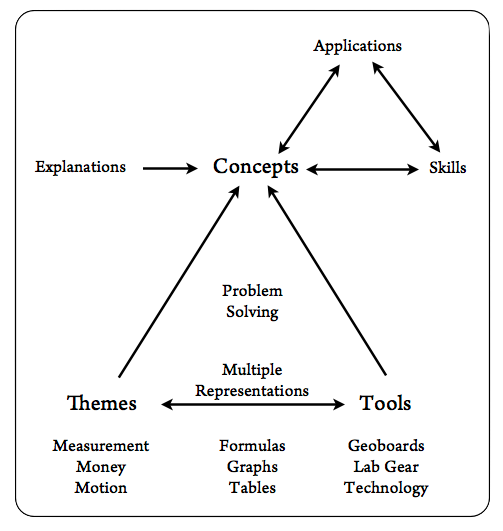
The above map is an attempt at a pedagogical model. Traditional teaching stays at the top, as it is based on the belief that skills practice and teacher explanations are sufficient to build student understanding. Understanding acquired this way, plus the skills, allow the student to apply the ideas.

Would that it were that simple.

In my experience, concepts are best developed by spending a lot of time at the bottom of the map. The interaction of themes, representations, and tools provides a foundation on which concepts can develop. (In the map, I mention examples of themes, representations, and tools. Of course, those lists are not meant to be exhaustive.)

The idea is not to rule out explanations and practice, but to give them a chance of being effective. Note that "Problem Solving" is at the center, as it needs to permeate the whole program: most activities should involve thinking.

This is pretty complicated, you say? Where does one start?

Forward design. For each unit, what tools are available? (Manipulative, technological.) What great curricula do you know of? Which books or websites have great problems on this topic? What representations are you familiar with that might throw light on the concept? what "real world" applications can you find? Who do you know who might be helpful in locating these things? Once you have the ingredients, you can chart a way to circulate through them in a way that makes sense mathematically and pedagogically. (For more on forward design, see this blog post, and The Assessment Trap.)

Themes are contexts that help ground the math in something that is meaningful to the student. They may be concrete (area, distance), "real world" (money, motion), or involve a story (growth and change, making comparisons).

Tables and graphs can help provide a concrete foundation to the study of functions and equations. This is sometimes described as modeling: you start with a concrete situation, use tables and graphs to think about it, and generalize with equations.

Tools. Kinesthetics and manipulatives do not accomplish miracles, but they can improve classroom discourse and provide meaningful and memorable reference points. In particular, algebra manipulatives can provide both access and depth to an essentially abstract subject, by way of a visual and geometric interpretation. (More about tools.)

I used this multidimensional approach in Algebra: Themes, Tools, Concepts, in Geometry Labs, and in my Algebra 2 materials. Follow the links to find many examples.

Start with definitions? No! Most students find it difficult to understand a definition for something they have no experience with. It is more effective to start with activities leading to concepts, and introduce vocabulary and notation when your students have some sense of what you're talking about. For example, the tangent ratio can be introduced with the help of slope, without having to mention trigonometry or the calculator, instead using the 10-centimeter circle. Once students can use the concept to solve problems, you can name it and reveal that there is a key on the calculator for it.

Anchor. Instead of definitions, start the unit with an interesting problem or activity (the anchor). It should be motivating and memorable, and it need not be easy. Examples of anchor activities are Geoboard Squares for the Pythagorean theorem (Lab 8.5 in Geometry Labs,) Rolling Dice for exponential functions, or Super-Scientific Notation for logarithms. A good anchor brings together key content with good practices, and generates curiosity and engagement. It is something you can refer to later on, to remind students of the basics of the unit.

Concrete or abstract? Math is all about abstraction, but understanding is almost always rooted in the concrete, so it is usually a good idea to start there. This can mean many things:

- Discrete first, continuous later.

- Numerical examples first, generalization later.

- Natural numbers to real numbers.

Almost any new idea is more accessible if you start with specific examples along these lines. For example, work on the geoboard (both the standard 11 by 11 geoboard, and the circle geoboard) is limited to particular examples based on the available pegs — but it lays the groundwork for a generalization using variables which would otherwise be impenetrable to many students.

From easy to hard? Well, that is certainly implied by the above. However, I will now challenge that assumption. (What can I say, sequencing curriculum doesn't lend itself to simple choices.) Avoid the trap of starting easy and gradually making it harder, for two reasons. One, starting too easy gives the wrong impression, and students don't launch into the unit with the right attitude. Two, gradually getting more difficult gives the impression to some students that there's a time where they might as well give up. Going back and forth is a way to keep everyone alert and challenged, and to have times where the pressure is lessened.

In fact, most of these guidelines are best implemented as a back and forth motion: for example, after introducing vocabulary and notation, one needs to re-introduce the concepts. Or, you should go back to numerical examples after having introduced a generalization. Likewise for most of these sequencing guidelines.

I hope this article provided useful guidelines for your big-picture planning. Whatever plan you end up with, consider it provisional, and don't lose sight of the reality that if it doesn't work, you can and should change it!